Motivating examples
- Mean estimation【回顾】:

 注:如果采取全部加起来÷N,数据量大时效率低;因此此时采取增量式以及迭代式的方法【来几个计算几个】来求解。
注:如果采取全部加起来÷N,数据量大时效率低;因此此时采取增量式以及迭代式的方法【来几个计算几个】来求解。
 注:迭代式算法!
注:迭代式算法!
- 关于迭代式算法的优缺点:增量式的方法【随着数据量大,wk精确逼近Ex】

 注:随机近似算法+随机梯度下降算法
注:随机近似算法+随机梯度下降算法
Robbins-Monro算法
- SA【随机近似】 定义:代表了随机【涉及对随机变量的采样】且迭代的算法——目的是进行方程的求解或者是求解优化问题
 注:SA不需要知道方程或者是目标函数的表达式,自然也不知道导数或者梯度的表达式
注:SA不需要知道方程或者是目标函数的表达式,自然也不知道导数或者梯度的表达式
- RM 算法:
 注:求解如下
注:求解如下
- Problem statement:g(w)=0

- 如何计算g(w)=0【未知g的表达式:如神经网络】
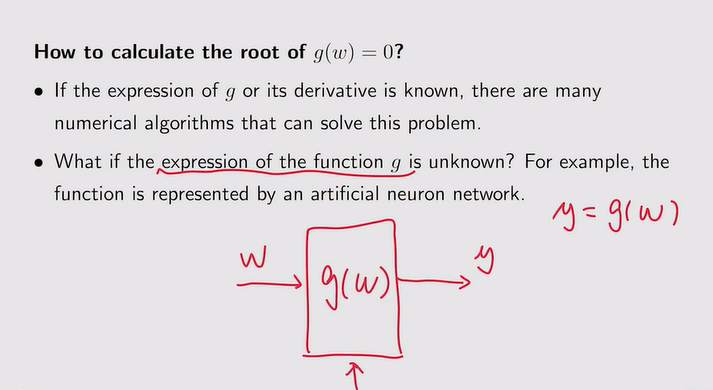
- 利用RM算法计算过程——没有模型【函数的表达式】时用数据的思想

- RM算法的收敛性

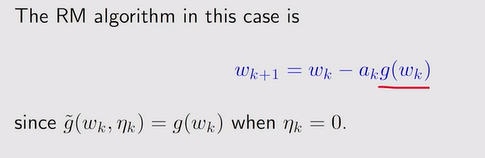
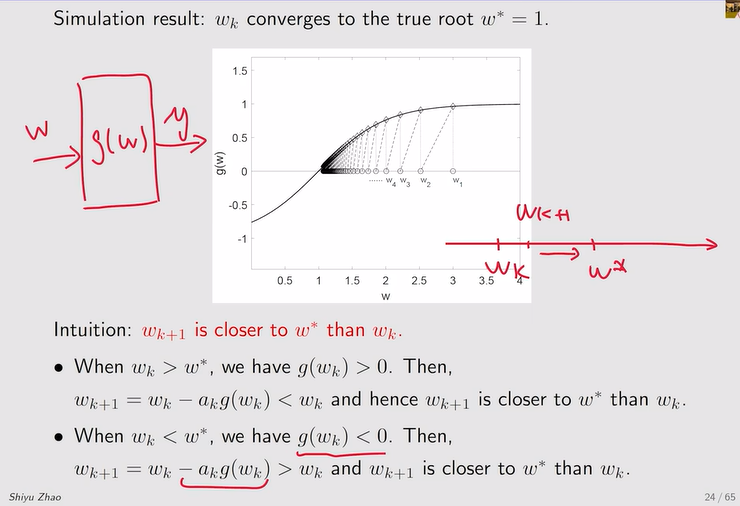 注:数学定理如下——满足条件1【关于gw的梯度】、条件2【关于系数ak】、条件3【关于测量误差的要求】才能保证RM算法的收敛性
注:数学定理如下——满足条件1【关于gw的梯度】、条件2【关于系数ak】、条件3【关于测量误差的要求】才能保证RM算法的收敛性
- 条件1:g函数保证单调递增,这才能保证g(w)=0有唯一解!

 注:相当于对J(w)求了二阶导得到一个Hessian matirx【正的矩阵——convexity(凸)】
注:相当于对J(w)求了二阶导得到一个Hessian matirx【正的矩阵——convexity(凸)】
- 条件2:ak最后趋向于0,且ak收敛到0的速度不会特别快【通常会选择一个非常小的常数赋给ak】
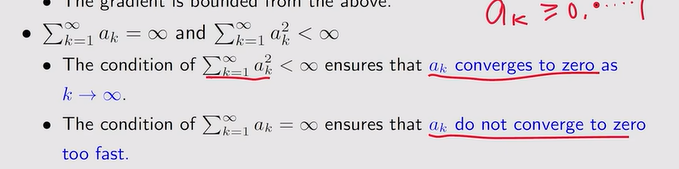

 注:上图表示w∞和w1有界,w1的值不能随便选——因此要满足ak的和为∞才保证w1的值随便选。
注:上图表示w∞和w1有界,w1的值不能随便选——因此要满足ak的和为∞才保证w1的值随便选。
- 条件3:

- RM算法的应用【mean estimation】



- Dvoretzkys 收敛算法:证明RM定理,且可以应用于Q-learning、TD learning

SGD【随机梯度下降】
- 梯度下降的定义:目标是找到最优的w使得这个函数J(w)达到最小

- 法一:无模型时,无法求期望

- 法二:缺点在于每一次更新wk时都要采样n次

- 法三:存在随机量的采样xk,相比BGD,就只用一个数据来估计【不精确】

- SGD算法举例:
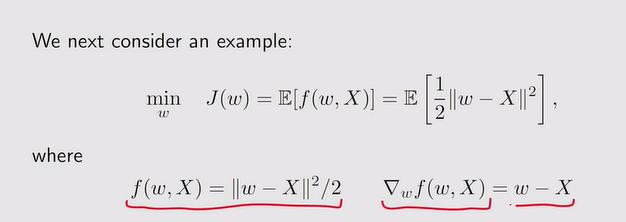


- SGD算法的收敛性:


 注:SGD是RM特殊的算法,相比GD,利用随机梯度代替真实梯度,结论如下:
注:SGD是RM特殊的算法,相比GD,利用随机梯度代替真实梯度,结论如下:
- SGD算法收敛的模式——相对误差:wk离w* 很近时才会体现随机性



- 无random varialble的SGD:

 注:此时把集合x定义为随机变量X【概率都是1/n】,如下【随机抽取】
注:此时把集合x定义为随机变量X【概率都是1/n】,如下【随机抽取】
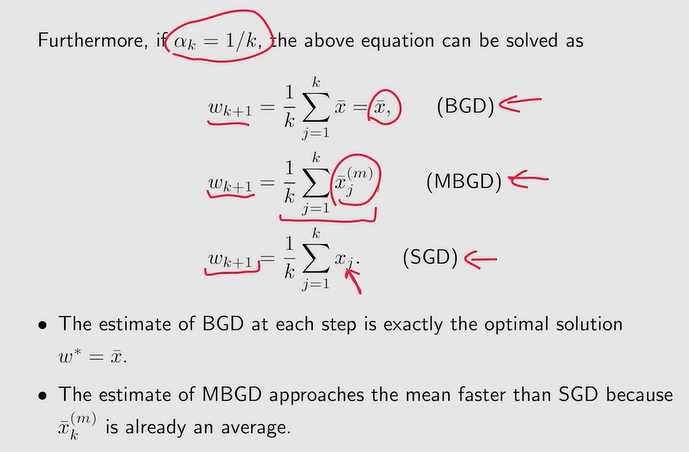
BGD、MBGD和SGD
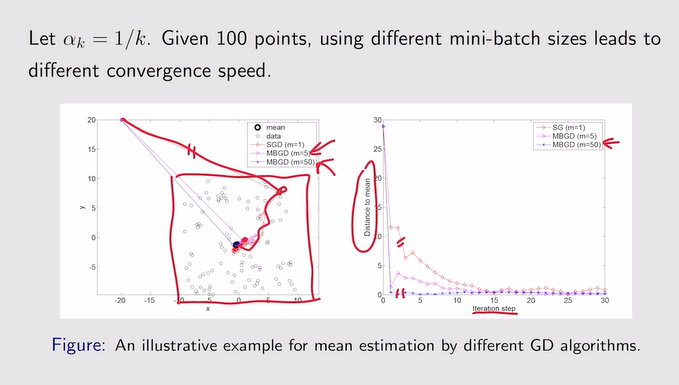
- 三个方法的区别:BGD最接近真实的期望,MBGD只是从所有数据中取一组,SGD是随机采样一个出来。

 注:蓝色字迹说明MBGD从n个样本中随机抽取n个可能会出现重复,而BGD是包含所有n。
注:蓝色字迹说明MBGD从n个样本中随机抽取n个可能会出现重复,而BGD是包含所有n。
- 例:

Summary

 注:如果采取全部加起来÷N,数据量大时效率低;因此此时采取增量式以及迭代式的方法【来几个计算几个】来求解。
注:如果采取全部加起来÷N,数据量大时效率低;因此此时采取增量式以及迭代式的方法【来几个计算几个】来求解。
 注:迭代式算法!
注:迭代式算法!
 注:随机近似算法+随机梯度下降算法
注:随机近似算法+随机梯度下降算法 注:SA不需要知道方程或者是目标函数的表达式,自然也不知道导数或者梯度的表达式
注:SA不需要知道方程或者是目标函数的表达式,自然也不知道导数或者梯度的表达式 注:求解如下
注:求解如下




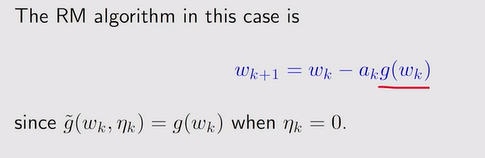
 注:数学定理如下——满足条件1【关于gw的梯度】、条件2【关于系数ak】、条件3【关于测量误差的要求】才能保证RM算法的收敛性
注:数学定理如下——满足条件1【关于gw的梯度】、条件2【关于系数ak】、条件3【关于测量误差的要求】才能保证RM算法的收敛性

 注:相当于对J(w)求了二阶导得到一个Hessian matirx【正的矩阵——convexity(凸)】
注:相当于对J(w)求了二阶导得到一个Hessian matirx【正的矩阵——convexity(凸)】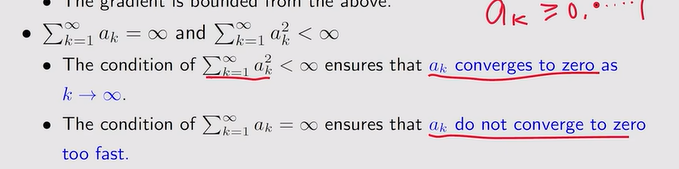

 注:上图表示w∞和w1有界,w1的值不能随便选——因此要满足ak的和为∞才保证w1的值随便选。
注:上图表示w∞和w1有界,w1的值不能随便选——因此要满足ak的和为∞才保证w1的值随便选。









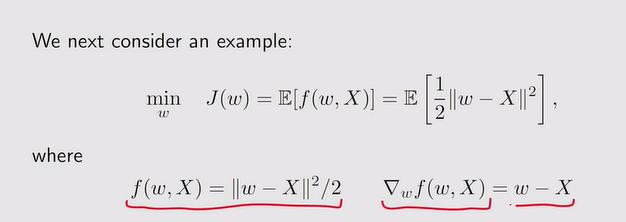




 注:SGD是RM特殊的算法,相比GD,利用随机梯度代替真实梯度,结论如下:
注:SGD是RM特殊的算法,相比GD,利用随机梯度代替真实梯度,结论如下:




 注:此时把集合x定义为随机变量X【概率都是1/n】,如下【随机抽取】
注:此时把集合x定义为随机变量X【概率都是1/n】,如下【随机抽取】

 注:蓝色字迹说明MBGD从n个样本中随机抽取n个可能会出现重复,而BGD是包含所有n。
注:蓝色字迹说明MBGD从n个样本中随机抽取n个可能会出现重复,而BGD是包含所有n。


