Motivating example
- 投硬币:

- 基于模型的:这么精确的模型我们可能无法知道!

- 无模型【大量采样+实验】:投掷硬币很多次,采样很多次,把采样求平均

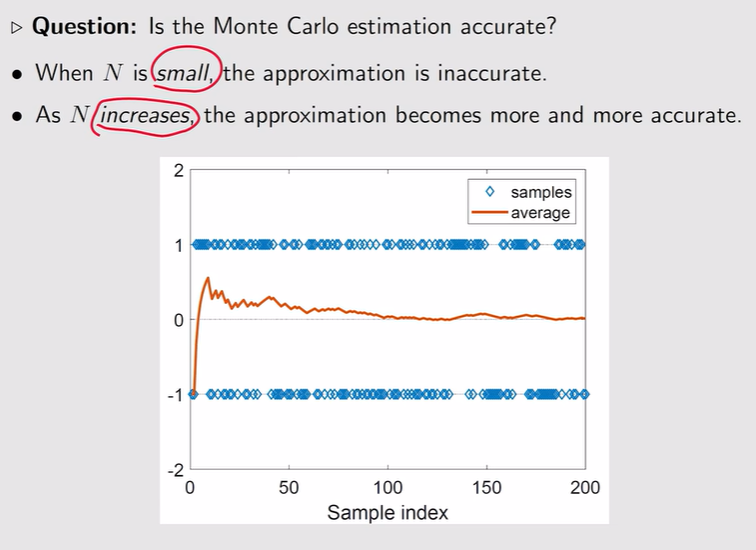 注:当N很小的时候不精确,当N越来越大的时候越来越精确【大数定理】
注:当N很小的时候不精确,当N越来越大的时候越来越精确【大数定理】
The simplest MC-based RL algorithm
- 值迭代到无模型的转变:

- Action value的计算——有模型+无模型
 注:无模型就是action value最初的定义,s状态下采取动作a得到return的期望
注:无模型就是action value最初的定义,s状态下采取动作a得到return的期望
- Monte Carlo estimation:

- The MC Basic algorithm:与有模型的值迭代最后一步都是一样的

 注:效率较低、不实用
注:效率较低、不实用
- 例:
- 简单例子:
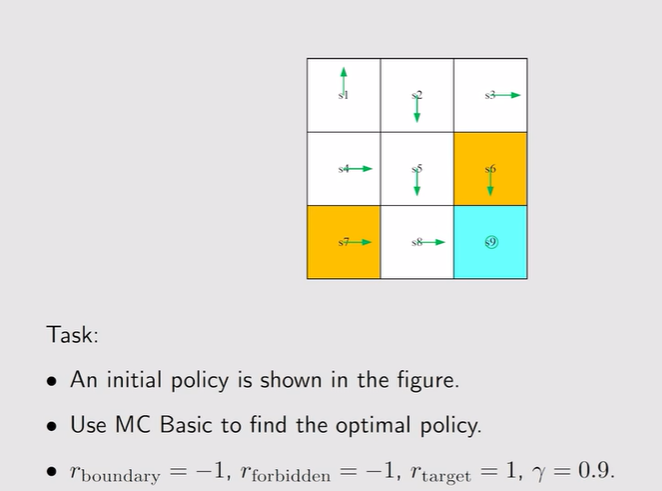





- Episode length:探索半径的长度,设置为几说明几步可以达到目标

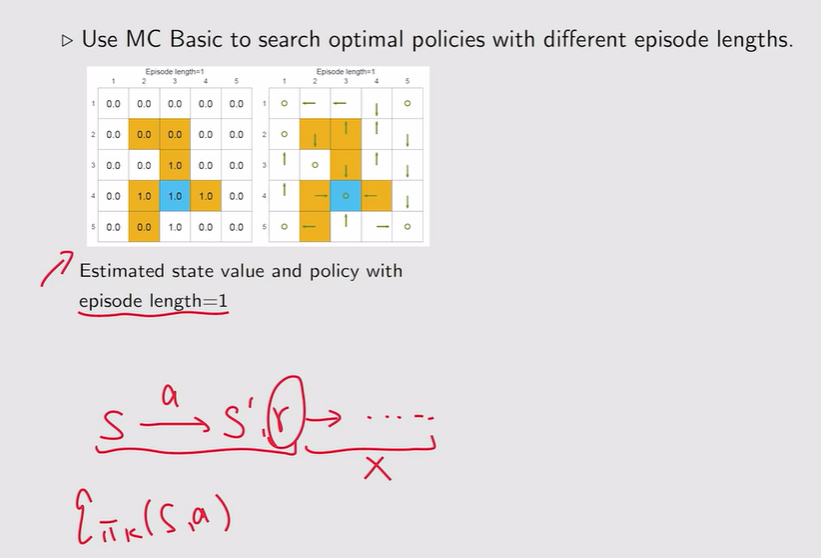 注:这里长度设置为1说明只走一次就停下【必须要求一步到位】,这时候得到的r作为return【估计不准确】
注:这里长度设置为1说明只走一次就停下【必须要求一步到位】,这时候得到的r作为return【估计不准确】
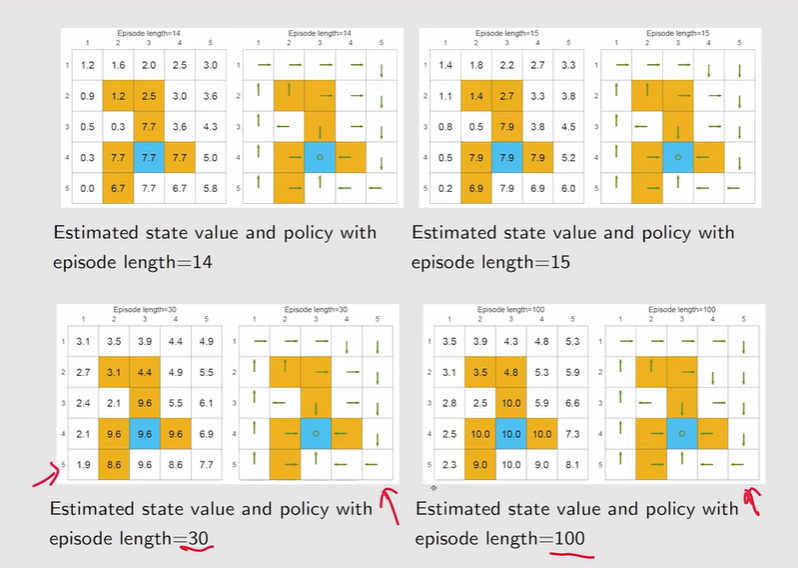 注:episode越大,optimal state value和真值就一模一样了
注:episode越大,optimal state value和真值就一模一样了
MC Exploring Starts
- Visit:在episode当中,每出现一个state-action pair都相当于对这个episode有一次访问 【MC-basic:Initial-visit method】

 注:对于first visit【第一次出现才能估计】出现一次s1,a2再出现一次就不能用它后面的episode来计算return;对于every-visit,每一次访问visit后面的episode都可以用来估计当前visit的return—q。
注:对于first visit【第一次出现才能估计】出现一次s1,a2再出现一次就不能用它后面的episode来计算return;对于every-visit,每一次访问visit后面的episode都可以用来估计当前visit的return—q。
- 策略更新:
- 法一:需要收集所有的episode并计算 average return【MC-Basic】

- 法二:只用一个episiode来立刻估计action value,然后直接开始改进策略

 GPI:策略评估【不需要把state/action value 精确估计出来】和策略提升交替切换
GPI:策略评估【不需要把state/action value 精确估计出来】和策略提升交替切换
- MC Exporing Starts:倒退计算提高效率

MC without exploring starts
- Soft policies:对每一个action都有可能做选择【episode比较长,从一个s/a出发就可以完全覆盖其他所有的s/a】
- ε-greedy:贪心选择于一个策略【概率最大】,但存在一定的探索性

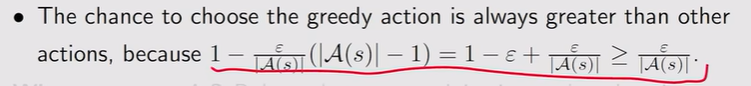
 注:Exploitation是充分利用——充分利用return大的;Exploration是探索,探索return可能大的其他action。
注:Exploitation是充分利用——充分利用return大的;Exploration是探索,探索return可能大的其他action。
- Greedy policy:从所有可能的策略做选择

- ε-Greedy policy:从ε-greedy策略中去找


- 例子:
- ε=1:探索性最强,只需要从某一些(s,a)出发就能覆盖到所有(s,a)
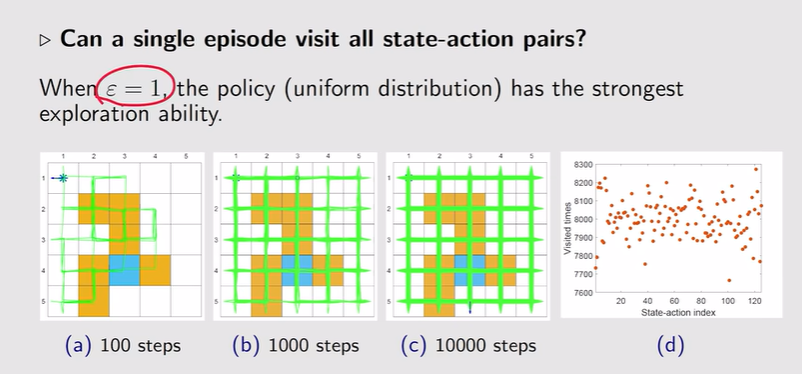
- ε偏小,偏好性强
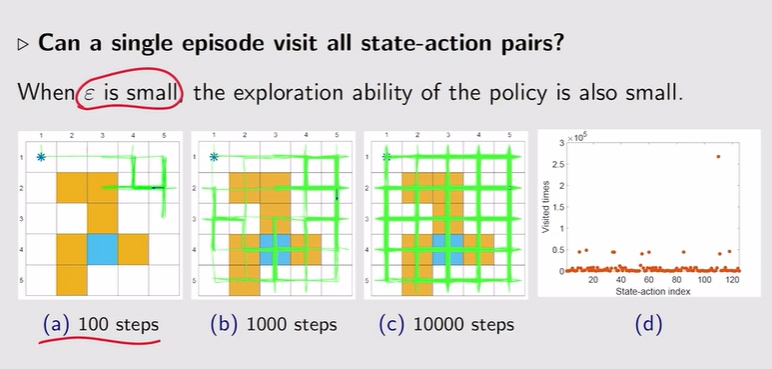
- MC ε-greedy:
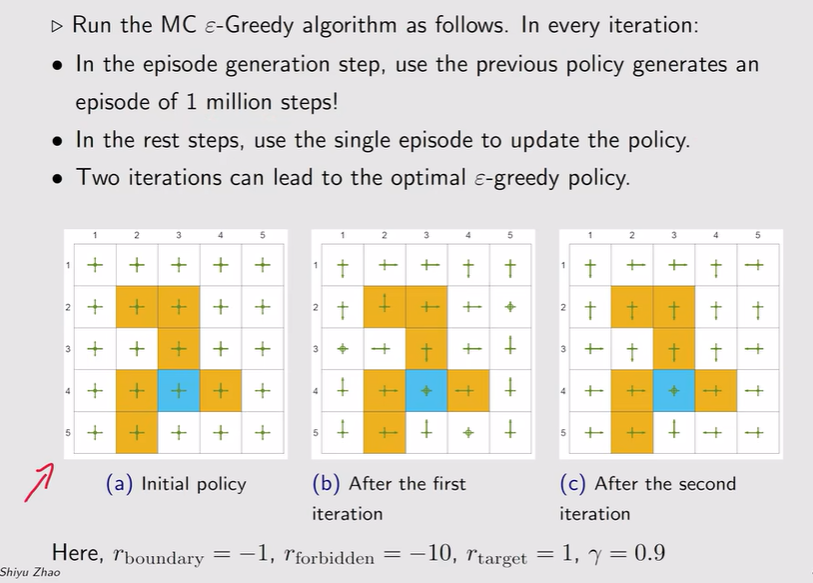

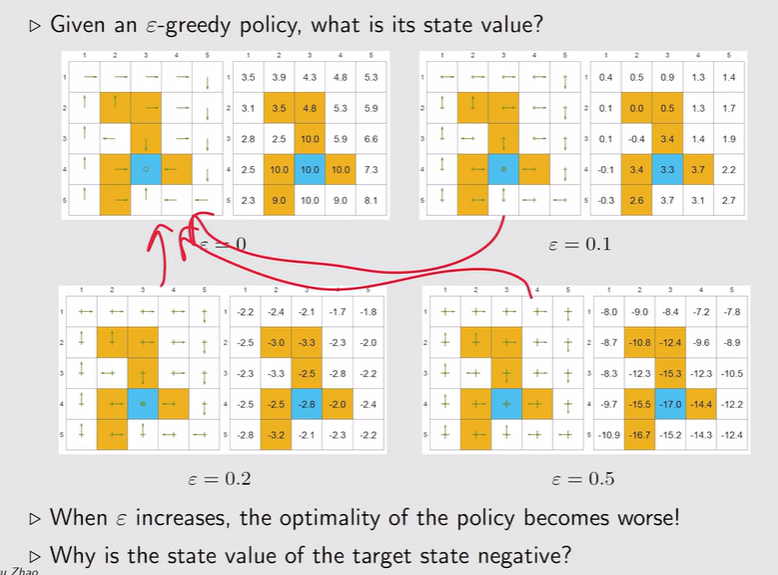 注:伴随ε的增大,最优性越来越差!——ε不能设置太大【上面的例子为0.1时,他的最优策略和greedy是一致的】;亦或者一开始ε比较大,后面逐渐变小——得到最优策略
注:伴随ε的增大,最优性越来越差!——ε不能设置太大【上面的例子为0.1时,他的最优策略和greedy是一致的】;亦或者一开始ε比较大,后面逐渐变小——得到最优策略
总结:



 注:当N很小的时候不精确,当N越来越大的时候越来越精确【大数定理】
注:当N很小的时候不精确,当N越来越大的时候越来越精确【大数定理】

 注:无模型就是action value最初的定义,s状态下采取动作a得到return的期望
注:无模型就是action value最初的定义,s状态下采取动作a得到return的期望

 注:效率较低、不实用
注:效率较低、不实用






 注:这里长度设置为1说明只走一次就停下【必须要求一步到位】,这时候得到的r作为return【估计不准确】
注:这里长度设置为1说明只走一次就停下【必须要求一步到位】,这时候得到的r作为return【估计不准确】
 注:episode越大,optimal state value和真值就一模一样了
注:episode越大,optimal state value和真值就一模一样了

 注:对于first visit【第一次出现才能估计】出现一次s1,a2再出现一次就不能用它后面的episode来计算return;对于every-visit,每一次访问visit后面的episode都可以用来估计当前visit的return—q。
注:对于first visit【第一次出现才能估计】出现一次s1,a2再出现一次就不能用它后面的episode来计算return;对于every-visit,每一次访问visit后面的episode都可以用来估计当前visit的return—q。

 GPI:策略评估【不需要把state/action value 精确估计出来】和策略提升交替切换
GPI:策略评估【不需要把state/action value 精确估计出来】和策略提升交替切换


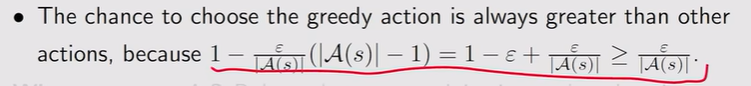
 注:Exploitation是充分利用——充分利用return大的;Exploration是探索,探索return可能大的其他action。
注:Exploitation是充分利用——充分利用return大的;Exploration是探索,探索return可能大的其他action。







 注:伴随ε的增大,最优性越来越差!——ε不能设置太大【上面的例子为0.1时,他的最优策略和greedy是一致的】;亦或者一开始ε比较大,后面逐渐变小——得到最优策略
注:伴随ε的增大,最优性越来越差!——ε不能设置太大【上面的例子为0.1时,他的最优策略和greedy是一致的】;亦或者一开始ε比较大,后面逐渐变小——得到最优策略