Return 的重要性
Return 可以评判哪个策略是最好的还是坏的!注 state value Return的计算 :注 Bootstrapping 【鞋带——讽刺异想天开——从自己出发不断迭代】贝尔曼公式 :一个状态的value依赖于其他状态的value。
State value
准备工作 :St【当前的状态】、At【当前状态下采取的动作】、Rt+1【得到的下一个reward,有时候也直接写成Rt】、St+1【跳到下一个状态】注 注 State value :是discounted return的期望,从不同的状态s出发【且采取不同的策略得到的轨迹不同也会导致期望不同】得到的期望也会不同,期望越大,说明从这个状态出发得到的价值越高,策略越好!注
贝尔曼公式
贝尔曼公式的定义:描述了不同状态 的state value之间的关系
推导过程:注 进而评估策略的好坏! 【其中,概率由模型决定】
例:得到方程组,求解不同的State value,下一步就是改进策略
策略1注
策略2注
贝尔曼方程——矩阵向量形式
矩阵向量形式 :由于n个状态可以有n个贝尔曼方程——因此可以写成矩阵向量的形式注 State value的求解:评估policy! 注 注
例:
好策略:不同的策略可以得到相同的state value
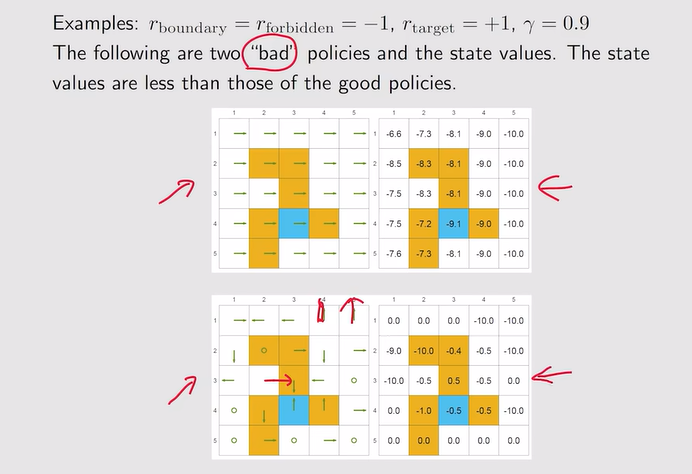
坏策略:
Action value
state value重温:从一个状态出发得到的average return
Action value 【action的价值】:从一个状态出发并且选择了一个action之后得到的average return,action value大的说明我采取这个动作可以获得更多的reward,我就在此时状态选择该动作注 例:所有的action都可以计算! ——虽然图示中告诉我们应该怎么走,但并不意味其他action的action value也是0,因为他给的路线不一定好,我们后续可能需要都评估一下【策略改进:通过比较,选择action value最大的】注
总结: 
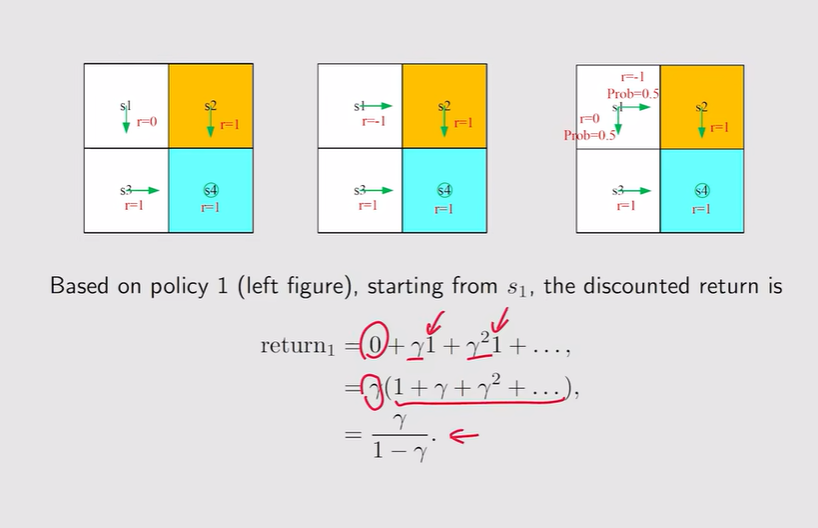

 注:Return3相当于从s1出发得到的一个平均return,即求期望——也就是state value
注:Return3相当于从s1出发得到的一个平均return,即求期望——也就是state value

 注:不同状态得到的return依赖于其他状态得到的return——Bootstrapping【鞋带——讽刺异想天开——从自己出发不断迭代】
注:不同状态得到的return依赖于其他状态得到的return——Bootstrapping【鞋带——讽刺异想天开——从自己出发不断迭代】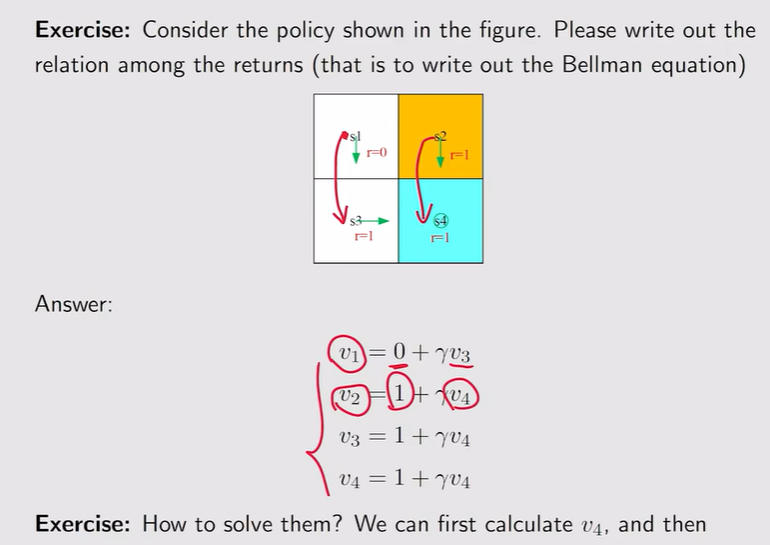

 注:随机变量意味着可以对它们求期望
注:随机变量意味着可以对它们求期望
 注:Rt+1是immediate reward
注:Rt+1是immediate reward 注:return和State value的区别在于——Return是对单个轨迹所求的,state value是从一个状态出发,对多个轨迹得到的return求平均【因此当当前状态所对应的策略是确定的,即轨迹只有一条,那么此刻二者没什么区别】
注:return和State value的区别在于——Return是对单个轨迹所求的,state value是从一个状态出发,对多个轨迹得到的return求平均【因此当当前状态所对应的策略是确定的,即轨迹只有一条,那么此刻二者没什么区别】



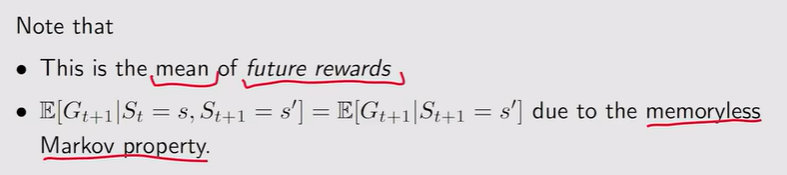
 注:对所有状态空间的所有状态都成立,有n个状态就有n个式子——把不同式子联立就可以计算state value——进而评估策略的好坏!【其中,概率由模型决定】
注:对所有状态空间的所有状态都成立,有n个状态就有n个式子——把不同式子联立就可以计算state value——进而评估策略的好坏!【其中,概率由模型决定】



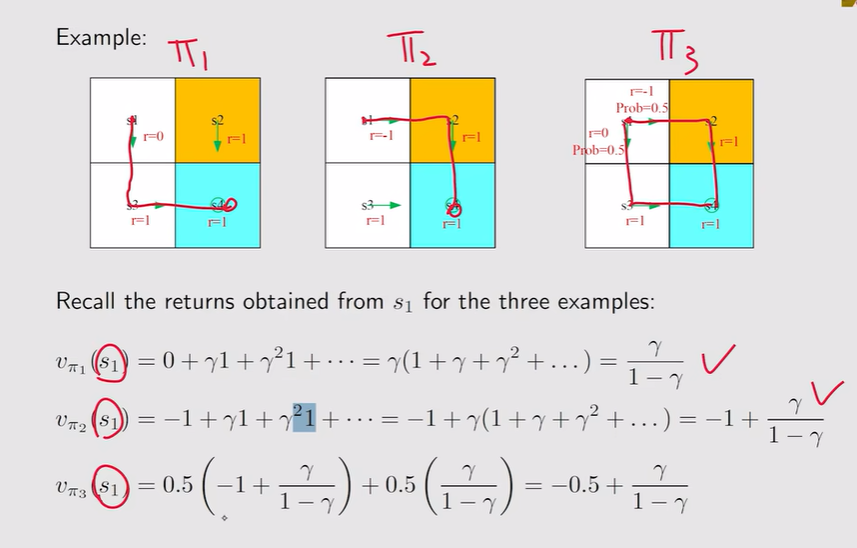
 注:S2、S3、S4价值高的因为他们离target比较近
注:S2、S3、S4价值高的因为他们离target比较近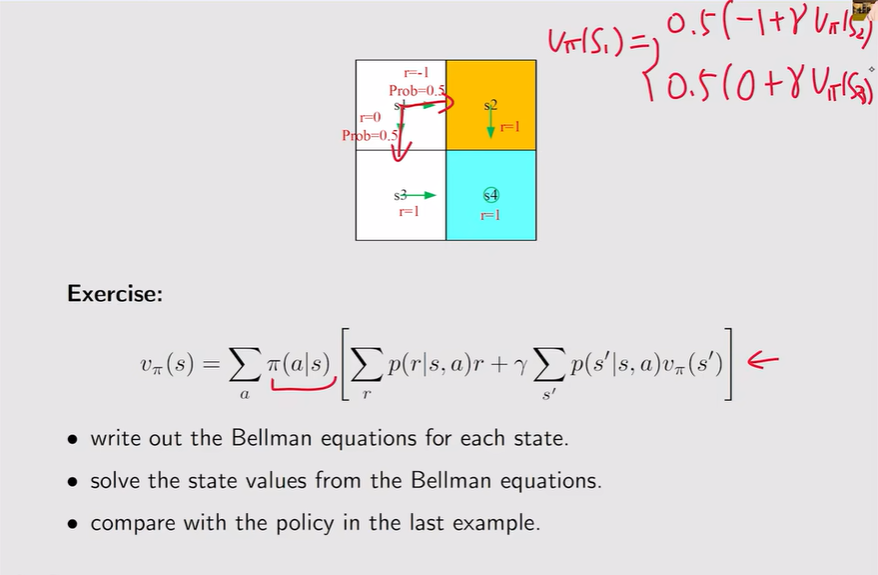
 注:Vπ(s1)比策略一低,说明还是策略一更好!
注:Vπ(s1)比策略一低,说明还是策略一更好!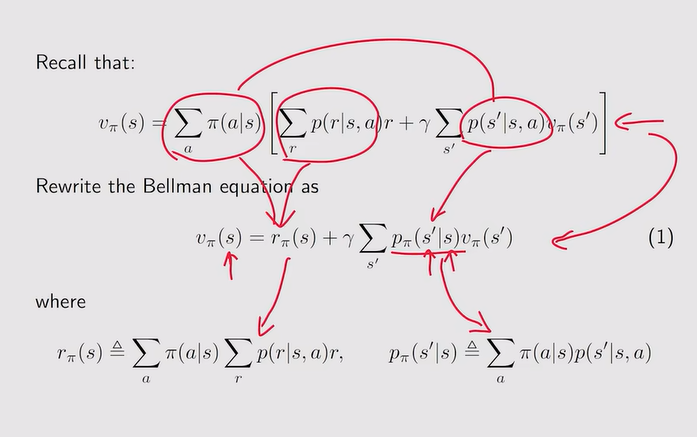
 注:Pπ为状态转移矩阵
注:Pπ为状态转移矩阵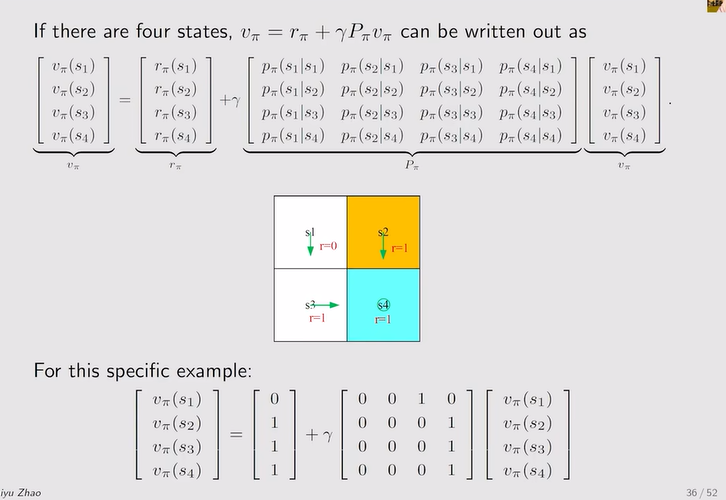
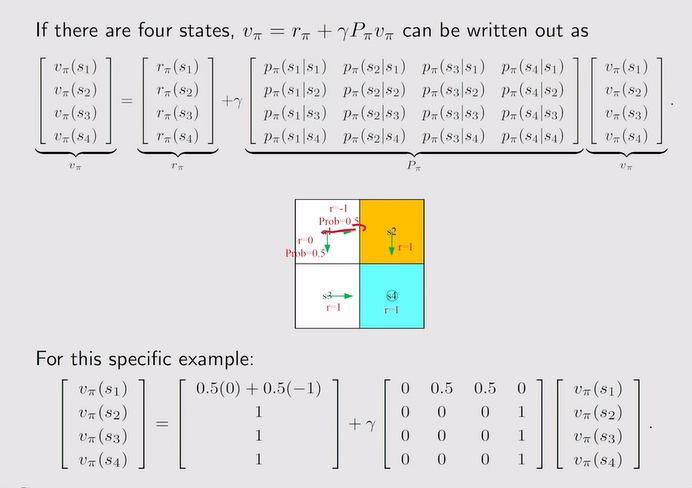

 注:迭代求state value,当k趋向于无穷,Vk近似于Vπ【真实的state value】
注:迭代求state value,当k趋向于无穷,Vk近似于Vπ【真实的state value】 注:证明σk=0
注:证明σk=0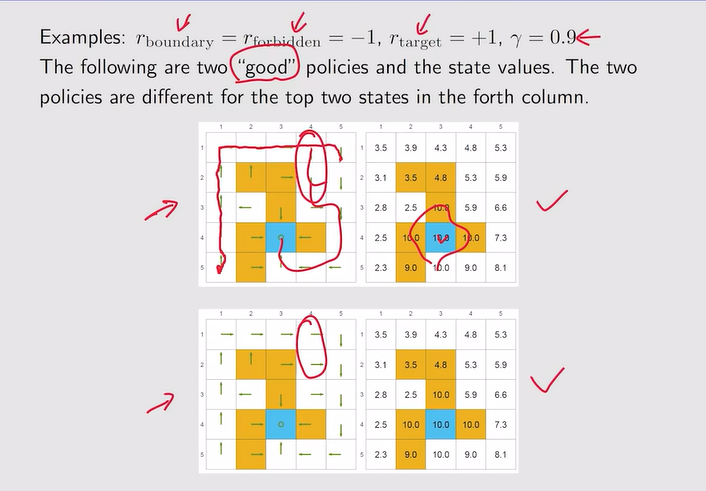

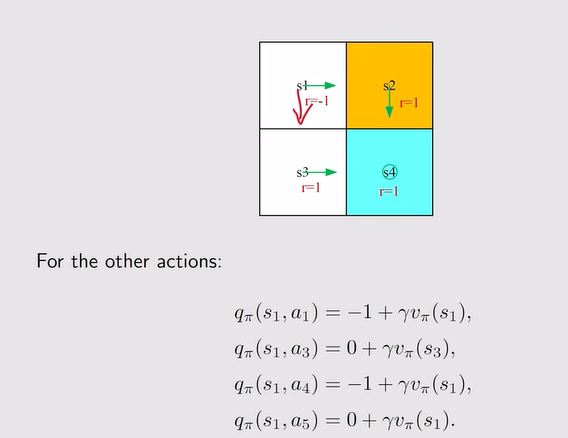
 注:不同的策略会得到不同的action value;下图所示的状态value相当于当前状态下采取不同action所得到action value的平均值
注:不同的策略会得到不同的action value;下图所示的状态value相当于当前状态下采取不同action所得到action value的平均值


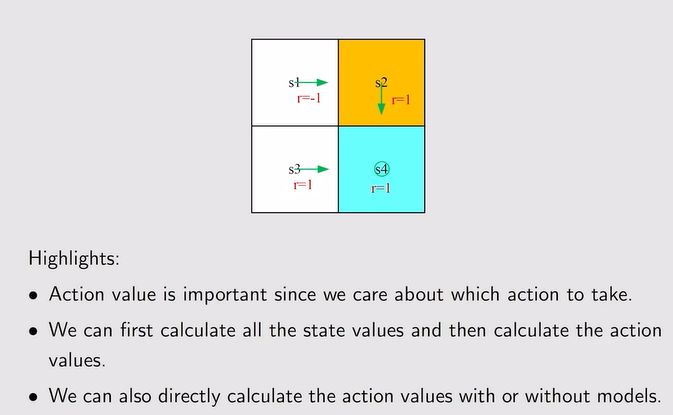 注:计算——先通过贝尔曼公式计算state value;直接计算action value【可以不依赖模型,通过数据就解出】
注:计算——先通过贝尔曼公式计算state value;直接计算action value【可以不依赖模型,通过数据就解出】