名词解释
- 随机变量:随机事件的数量表现,随机事件数量化的好处是可以用数学分析的方法来研究随机现象。

- 线性可分与线性不可分:

- 机器学习:


- 激活函数:


数学基础
- 最小二乘法求多元线性回归的目标函数最优解:
 注:arg min使后面这个式子达到最小值时的变量的取值。
注:arg min使后面这个式子达到最小值时的变量的取值。
- 向量:
 注:向量的转置就是向量的行变成列(行和列互换)的意思
注:向量的转置就是向量的行变成列(行和列互换)的意思
- 张量:

- 矩阵:



- 矩阵的秩:

- 矩阵的逆:


- 矩阵的分解:

- 特征分解:

- 奇异值分解:

- 最小二乘法:【回归问题】它通过最小化误差的平方和寻找 数据的最佳函数匹配。

- 概率分布:


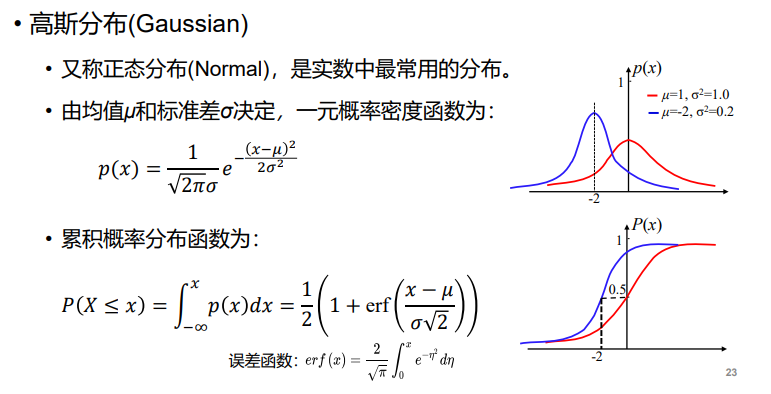
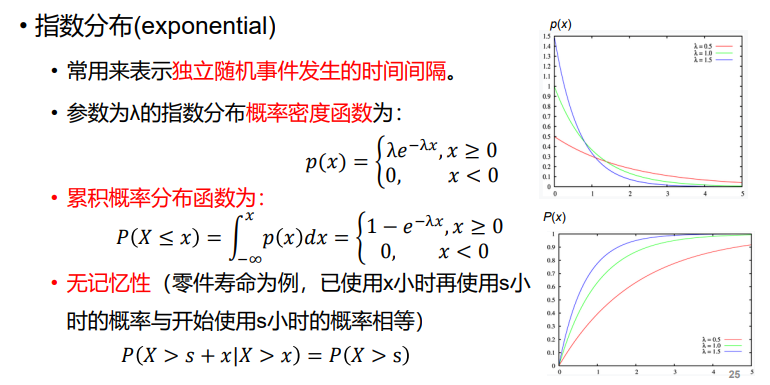
- 概率定义:


- 概率公式:

- 常用统计量:
- 期望:在概率和统计学中,数学期望是试验中每次可能结果的概率乘以其结果的总和,反映随机变量平均值的大小

- 方差:随机变量与数学期望之间的偏离程度

- 协方差:衡量两个随机变量X和Y之间的总体误差

- 损失函数:将随机事件或其有关随机变 量的取值映射为非负实数以表示该随机事件的“风险” 或“损失”的函数




- 回归问题中的损失函数:

- 分类问题损失函数:



- 信息论
- 熵增定律:孤立系统总是趋向于熵增,最终达到熵的最大状态,也就是系统的最混乱无序状态。但是,对开放系统而言,由于它可以将内部能量交换产生的熵增通过向环境释放热量的方式转移,所以开放系统有可能趋向熵减而达到有序状态。
- 信息熵:样本集合纯度一种指标,也可以认为是样本集合包含的平均信息量
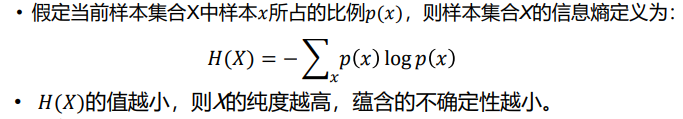
- 联合熵:两个随机变量X和Y的联合分布可以形成联合熵,用来度量二维随机变量 X,Y的不确定性
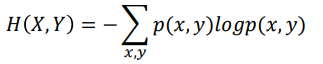
- 条件熵:

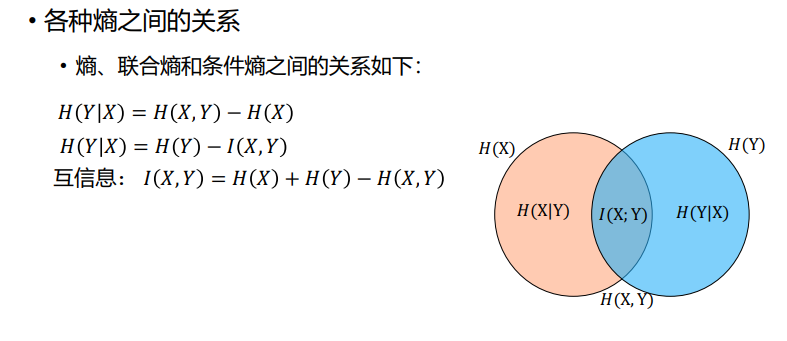
- 相对熵:KL散度

机器学习基础
- 数据集:

- 数据集分类:


- 误差:

- 过拟合与欠拟合:

- 机器学习分类
- 无监督:

- 聚类:对一批没有类别标签的样本集,按照样本之间的相似程度分类, 相似的归为一类,不相似的归为其它类。这种分类称为聚类分析,也称为无监督分类。目的是“将数据分成多个类别,在同一个类内,对象 (实体)之间具有较高的相似性,在不同类内,对象之间具有较大的差异性”。

- 降维:目的是“将原始样本数据的维度𝑑降低到一个更小的数𝑚,且尽量使得样本蕴含信息量损失最小,或还原数据时产生的误差最小”。


- 有监督:

- 线性回归:最小二乘法求损失函数

- 逻辑回归:sigmoid函数

- 支持向量机:



- 决策树:是一种基于树结构进行决策的机器学习方法,这恰是人类面临决策时一种很自然的处理机制。
 注:信息增益就代表熵增
注:信息增益就代表熵增
- 随机森林:该算法用随机的方式建立起一棵棵决策树,然后由这些决策树组成一个森林,其中每棵决策树之间没有关联。


神经元模型——M-P模型: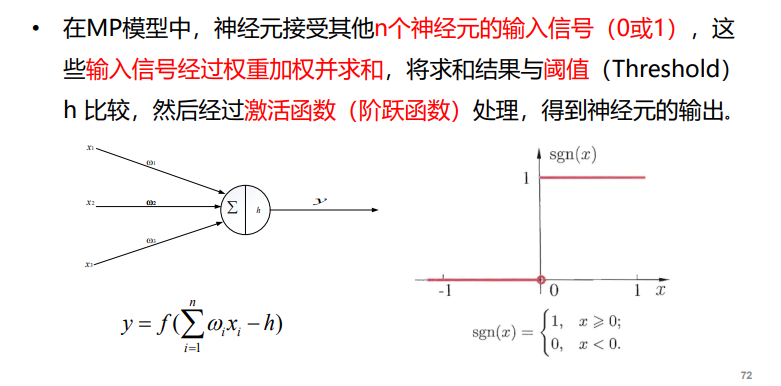
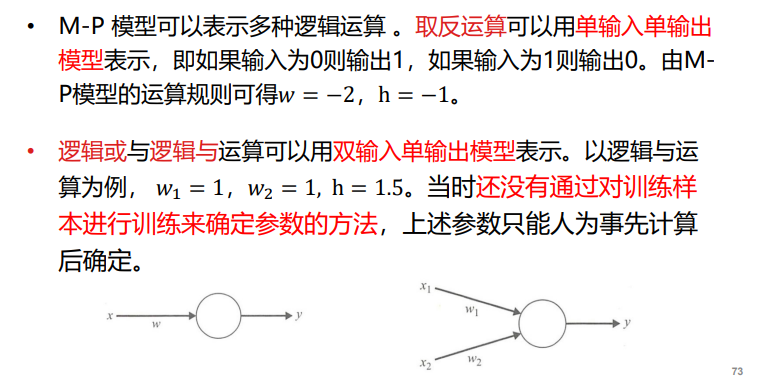

感知器以及多层感知器
- 感知器定义:与 M-P模型需要人为确定参数不同,感知器能够通过训练自动确定参数。训练方式为有监督学习,即需要设定训练样本和期望输出,然后调整实际输出和期望输出之差的方式(误差修正学习)。



- 训练过程:

- 感知器与线性问题:
- 单层感知器:只有一个神经元


- 多层感知器:

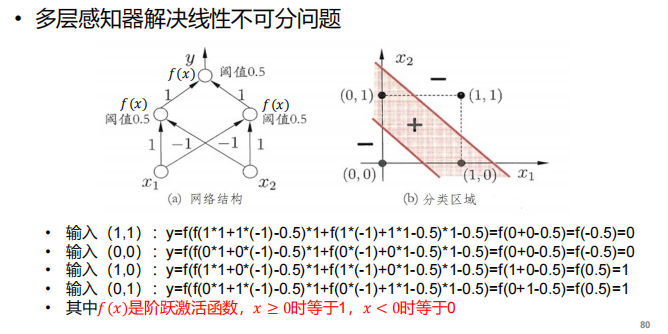
BP算法
- 定义:
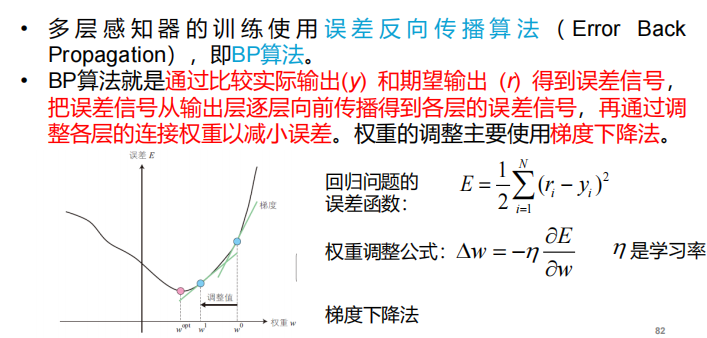

- BP算法的瓶颈以及解决方案:

 注:这里阐释了激活函数的重要性以及为什么不用MP模型的阶跃函数做激活函数。
注:这里阐释了激活函数的重要性以及为什么不用MP模型的阶跃函数做激活函数。
- BP算法的例子:
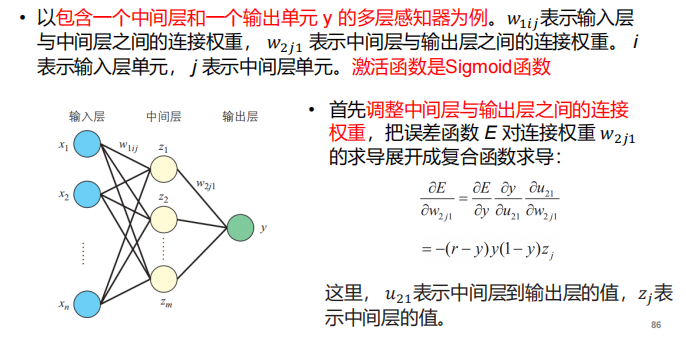


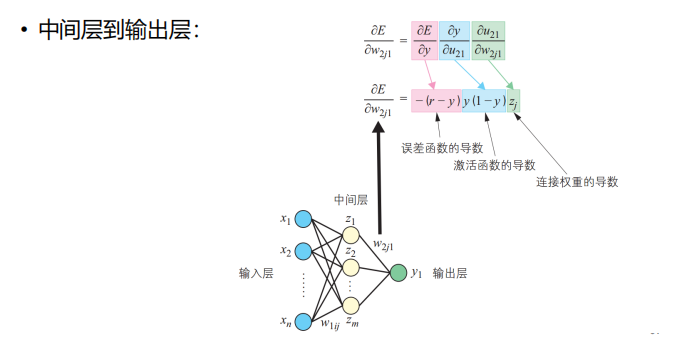






 注:arg min使后面这个式子达到最小值时的变量的取值。
注:arg min使后面这个式子达到最小值时的变量的取值。
 注:向量的转置就是向量的行变成列(行和列互换)的意思
注:向量的转置就是向量的行变成列(行和列互换)的意思




























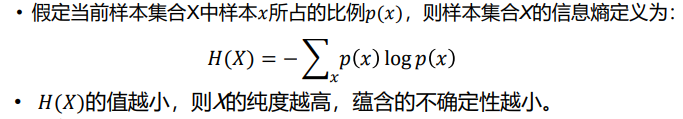
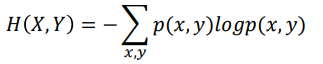


















 注:信息增益就代表熵增
注:信息增益就代表熵增
















 注:这里阐释了激活函数的重要性以及为什么不用MP模型的阶跃函数做激活函数。
注:这里阐释了激活函数的重要性以及为什么不用MP模型的阶跃函数做激活函数。


