策略梯度方法——西湖大学

Policy gradient

1. 查表法【策略】：
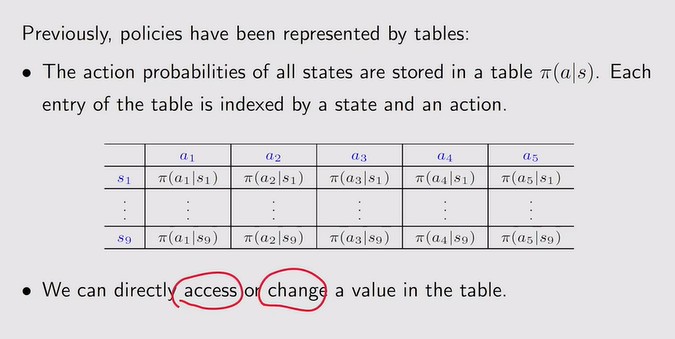
2. 表格——函数【参数：θ】：泛化能力的增强注：函数法需要我们定义一个标量的目标函数，然后去优化这个目标函数注：概率对于函数需要计算注：需要改变θ才能更新策略
3. Policy gradient基本思路：

Metrics to define optimal policies

1. Average value：策略的函数
   1. d和策略独立：
   2. d和策略非独立：根据策略——访问多的权重大，访问少的权重小
2. Average reward：策略的函数【immediate r】注：s0可以省略，因为最后s0不起作用
3. Metric补充：
   1. 上述的V以及R都是θ的函数，因此需要更新θ来最优化这两个metrics
   2. 
   3. 二者关系：
   4. 拓展：J(θ)=v(π)平均

Gradients of the metrics

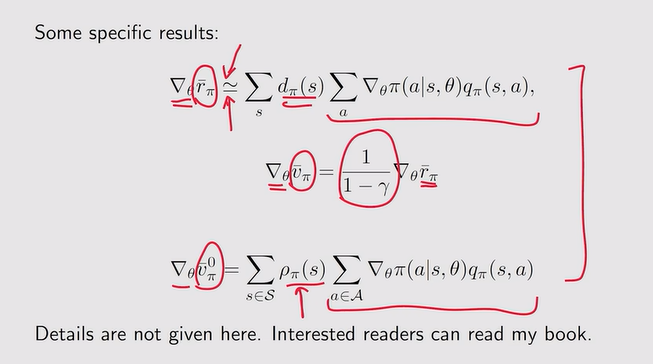
1. 梯度定义：注：通过采样来近似梯度
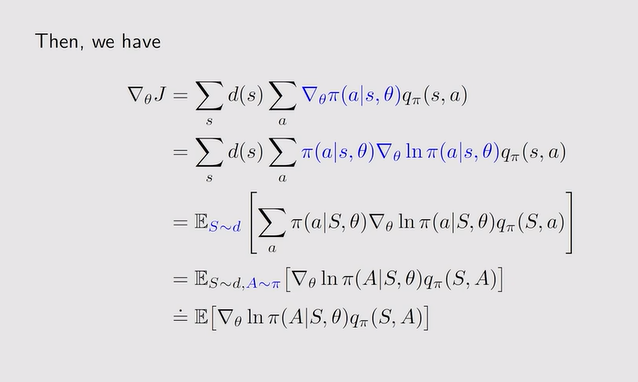
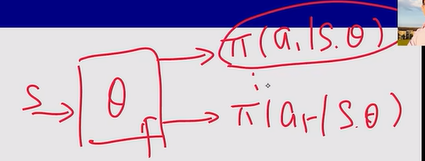2. 归一化处理：softmax函数——策略是探索性的注：h(s,a,θ)是一个特征函数注：若action为无穷多个就不适用

Reinforce

1. 梯度上升：随机梯度替代真实梯度，但qπ(st,at)也是未知的——蒙特卡洛

   1. 如何采样？
   2. 梯度上升：通过改变θ来优化π(at|st,θ)注：探索和充分利用的平衡——βt

2. Reinforce：基于蒙特卡洛进行策略更新

3. Summary