Motivating examples
- RM算法求mean回顾:



TD learning of state values
- TD算法做policy evaluation:首先根据策略π生成一组数据,TD算法就是要用这些数据来估计π对于的state value



- TD target:使得V(St)朝着TD target的方向改进,即下一时刻的V(St+1)更接近TD target

- TD error:为什么叫时序差分——error【两个时间步骤的差异】

- TD算法性质:policy evaluation——估计state value

TD算法的收敛性
- TD算法的数学性质:在没有模型的情况下求解贝尔曼公式


 注:贝尔曼需要持续的采样(s,r,s’),且Vπ未知,解决方法如下
注:贝尔曼需要持续的采样(s,r,s’),且Vπ未知,解决方法如下

- TD算法收敛性分析:αt的和为无穷说明被访问了很多次

- 与MC-learning的比较:TD-learning【一次采样,涉及的随机变量少,因此variance小,但是bias大!初始不准确的估计可能会进入后面的估计中,但随着数据量的增大,bias会被抵消】可以实时更新value,但MC需要等到episode完成才可以求value

 注:bootstrapping说明一开始我对下一个时刻的value有猜测,根据采样来实时更新猜测
注:bootstrapping说明一开始我对下一个时刻的value有猜测,根据采样来实时更新猜测
Sarsa
- 前情回顾:当我们要改进策略时,需要估计action value,这样的话那个value大选择哪一个策略
- Sarsa:——对于给定策略进行Action value的估计:
 注:解决的数学问题【求解了贝尔曼公式】如下:
注:解决的数学问题【求解了贝尔曼公式】如下:

- Sarsa【policy evaluation——求action value】+policy improvment:改进策略,得到策略后产生新的experience,然后继续迭代

- 例:从特定的状态到目标状态路径的最优策略!

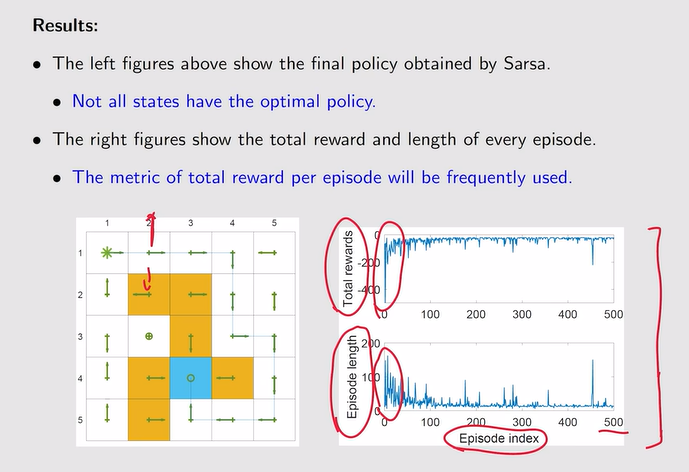
Expected Sarsa
- 定义:在St+1时刻有很多动作a可以选择,因此St+1的动作价值函数可以用期望的形式表示,得到state value【这里就不是一个action value了】


- 数学性质:还是求解贝尔曼公式
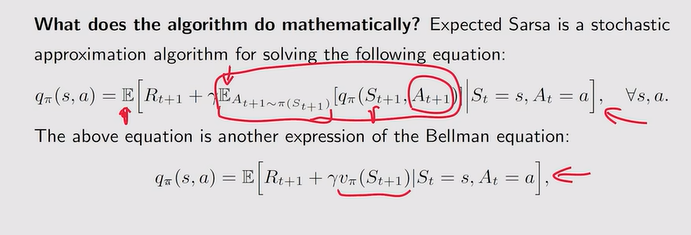
n-step Sarsa
- 定义:包含了蒙特卡洛和Sarsa


- n-step性质:需要等到t+n时刻,才能更新qt+1

Q-learing
- 与TD的区别:直接估计optimal action value——不需要做policy evaluation和 policy improvement 这两个之间来回交替运行,它直接把最优的action value估计出来了。
- 定义:每一个状态看看哪一个action的q比较大就选择这个q

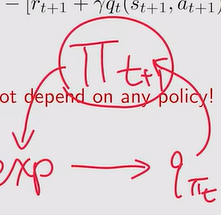
- 解决的数学问题:求解贝尔曼最优方程

- 性质:off-target

- Off-policy and on-policy:
- Behavior策略与环境进行交互生成experience
- target policy——一直在更新,最后会得到我们想要的最优策略
- 二者相同时为on-policy【用这个策略与环境进行交互得到experience,同时再改进这个策略】,反之Off二者可以不同【这有助于我们利用别人的经验来进行学习】

- 如何判断:

- Sarsa:on-policy【用πt来估计action value,后面用action value来更新πt从而得到更好的策略,所以πt二者皆是】

- MC-learning:on-policy

- Q-learning:off-policy


- Q-learing算法实施:
- on-policy vision:Target policy can be anything【存在一个搜索】和behaviour一样

- off-policy vision:

- 例:

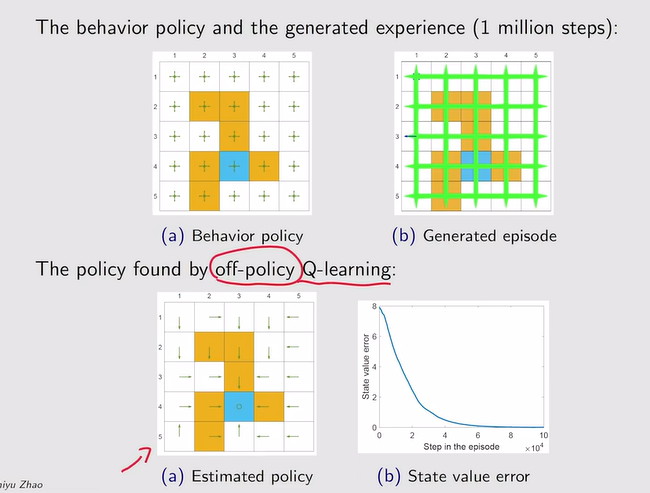 注:上图为探索性比较强的例子,下面为探索性较弱的例子
注:上图为探索性比较强的例子,下面为探索性较弱的例子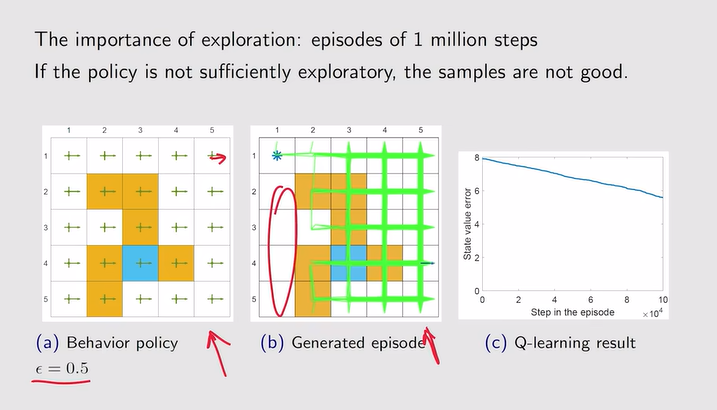
A unified point of view【总结】:
- 总结:













 注:贝尔曼需要持续的采样(s,r,s’),且Vπ未知,解决方法如下
注:贝尔曼需要持续的采样(s,r,s’),且Vπ未知,解决方法如下



 注:bootstrapping说明一开始我对下一个时刻的value有猜测,根据采样来实时更新猜测
注:bootstrapping说明一开始我对下一个时刻的value有猜测,根据采样来实时更新猜测
 注:解决的数学问题【求解了贝尔曼公式】如下:
注:解决的数学问题【求解了贝尔曼公式】如下:






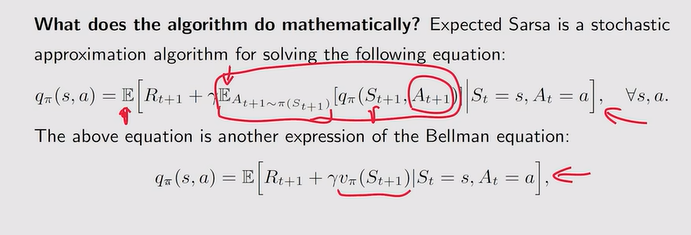
















 注:上图为探索性比较强的例子,下面为探索性较弱的例子
注:上图为探索性比较强的例子,下面为探索性较弱的例子

