波动光学成像原理显微镜分辨率

光的波粒二象性

1. 波动性：杨氏双缝实验、光极性实验(Maxwell: 电磁波在真空中以光速传播，即光是电磁波)
   • . 电子双缝干涉实验：
2. 粒子性：光电转化实验(爱因斯坦: 光的能量与波长有关，以光量子的形式存在。即光是光子)
3. 德布罗意的波粒二相性假说:

光的干涉和衍射

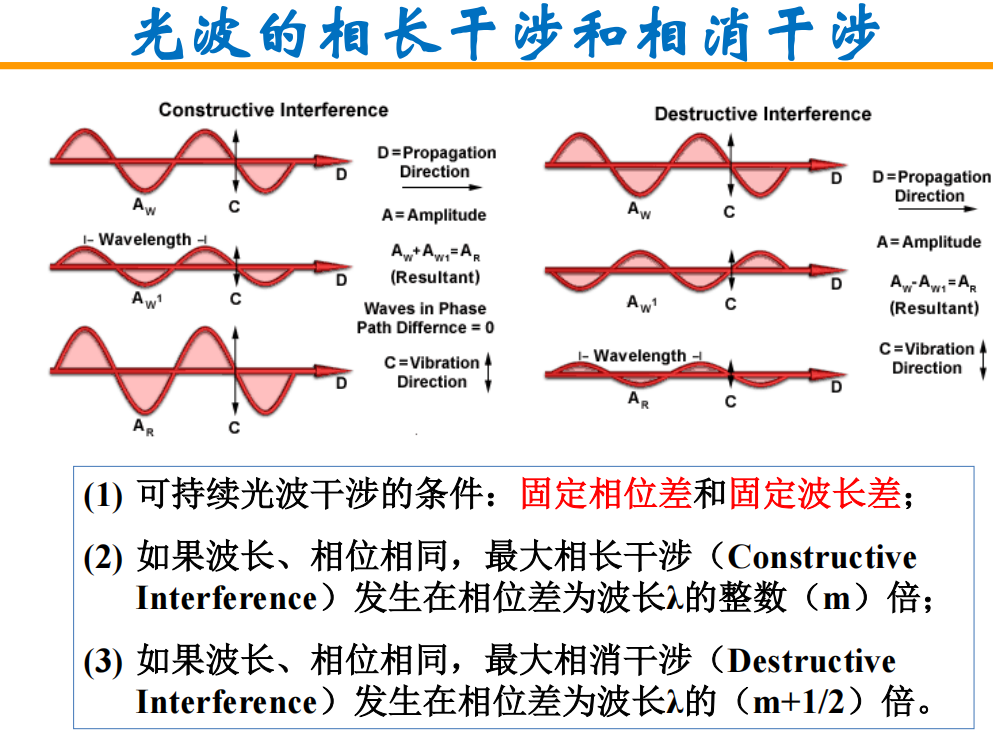
1. 干涉*：两列或几列光波在空间相遇时相互叠加，在某些区域始终加强，在另一些区域则始终削弱，形成稳定的强弱分布的现象，证实了光具有波动性。
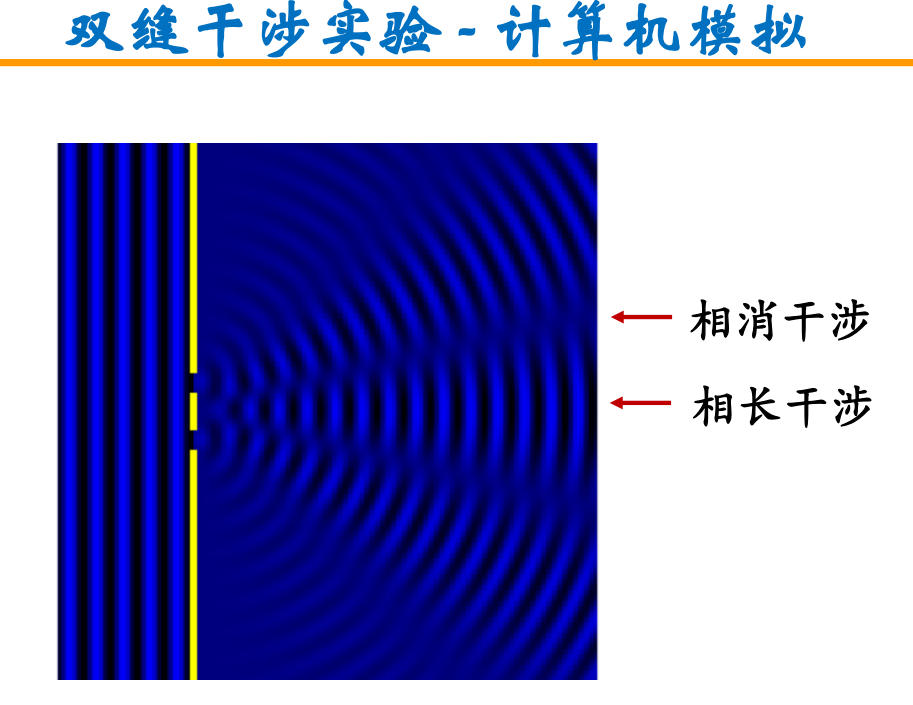
   • 计算机模拟的双缝干涉实验：二者的分布规律决定了分辨率
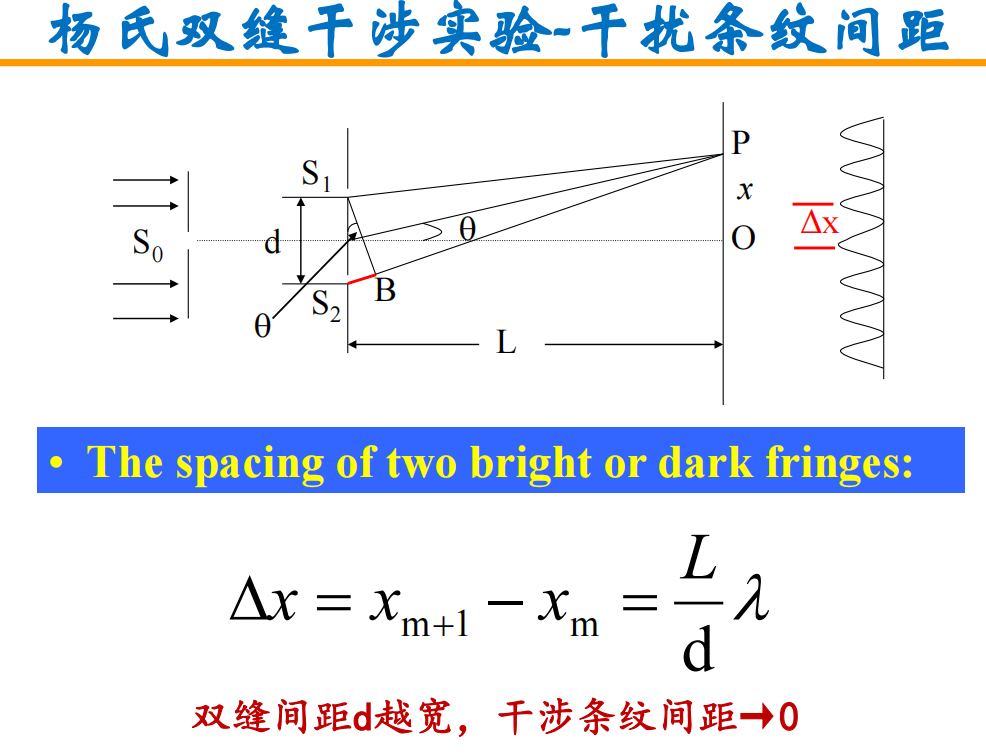
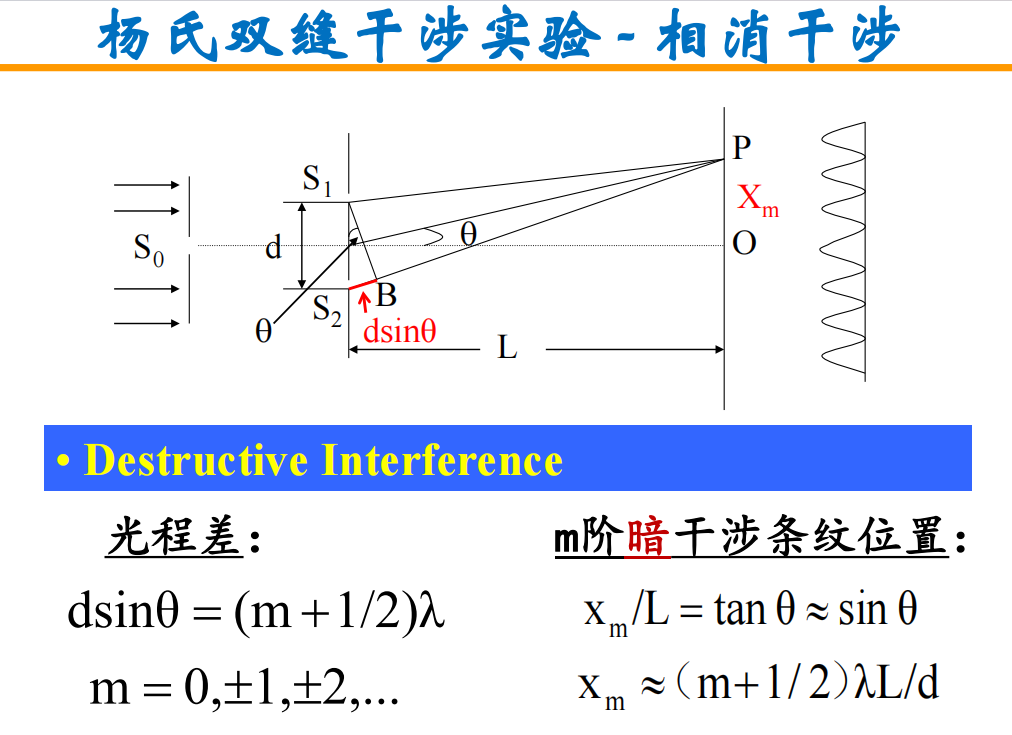
   • 杨氏双缝干涉实验：可通过亮条纹的位置预测光的波长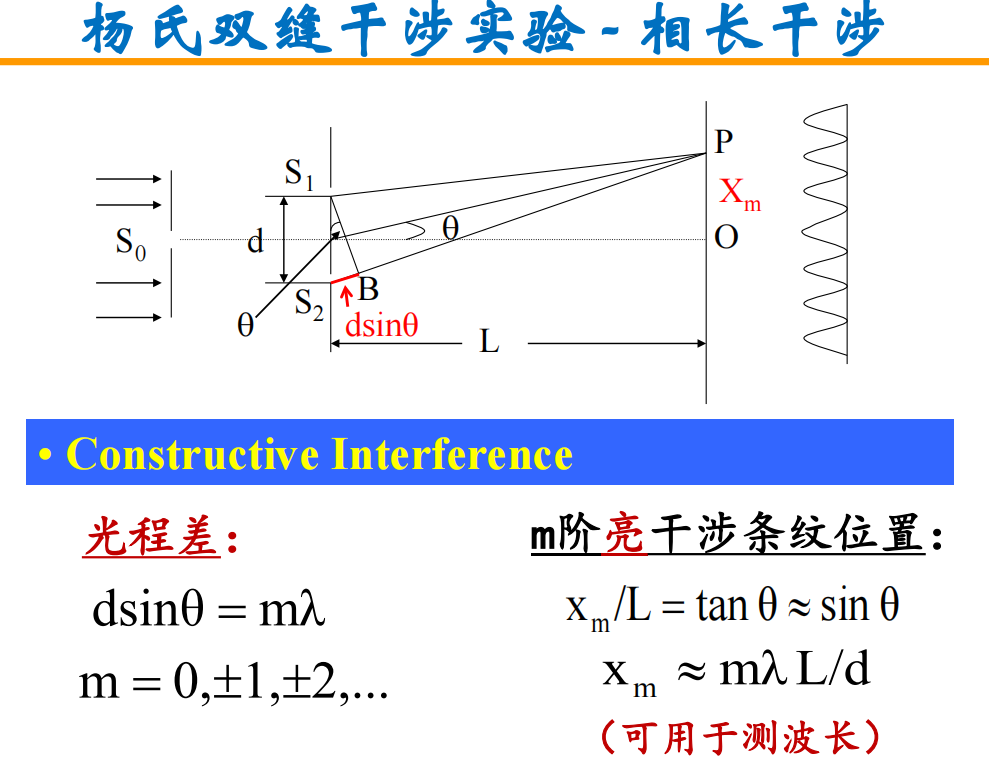光程差计算过程如下：
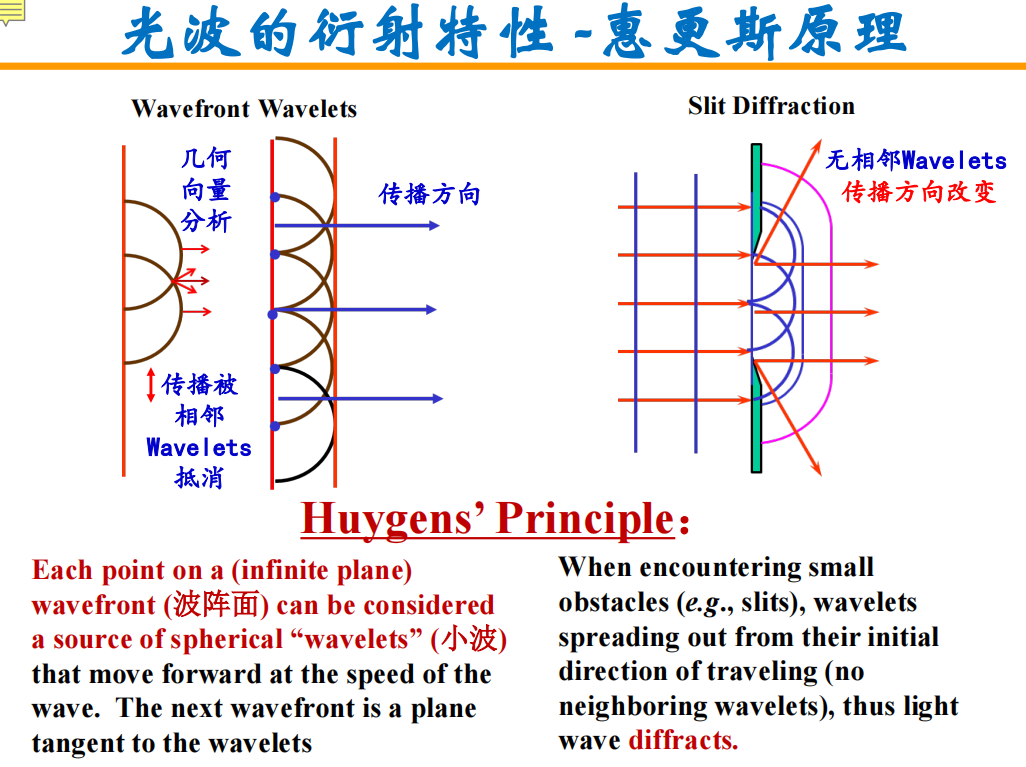
2. 衍射：光传播方向的改变
   • 如何理解光传播方向的改变？
     • 光波的传播(小波Wavelets模型)：相当于每一个球面上的点又是一个点光源
     • 光波传播方向的改变：无相邻的Wavelets
   • 衍射的分类以及条纹的推导：
     • 分类：
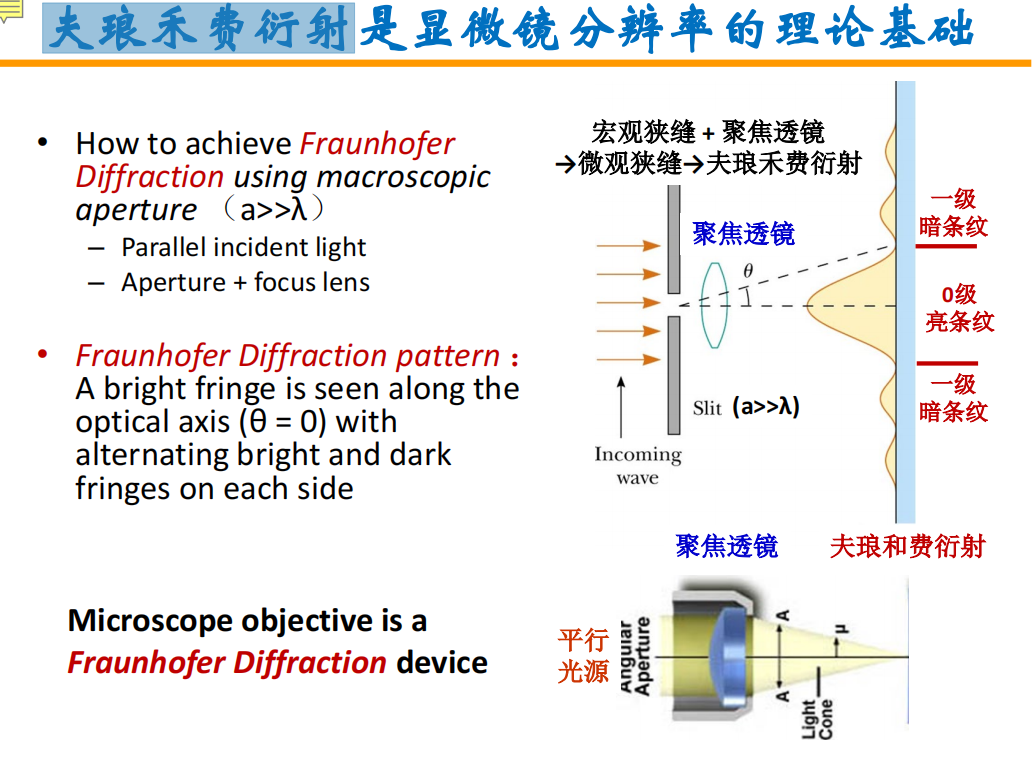
     • 远场衍射的推导（光波的单缝衍射近似无数对杨氏双缝干涉的叠加；相消衍射：光程差必须是波长的一半）
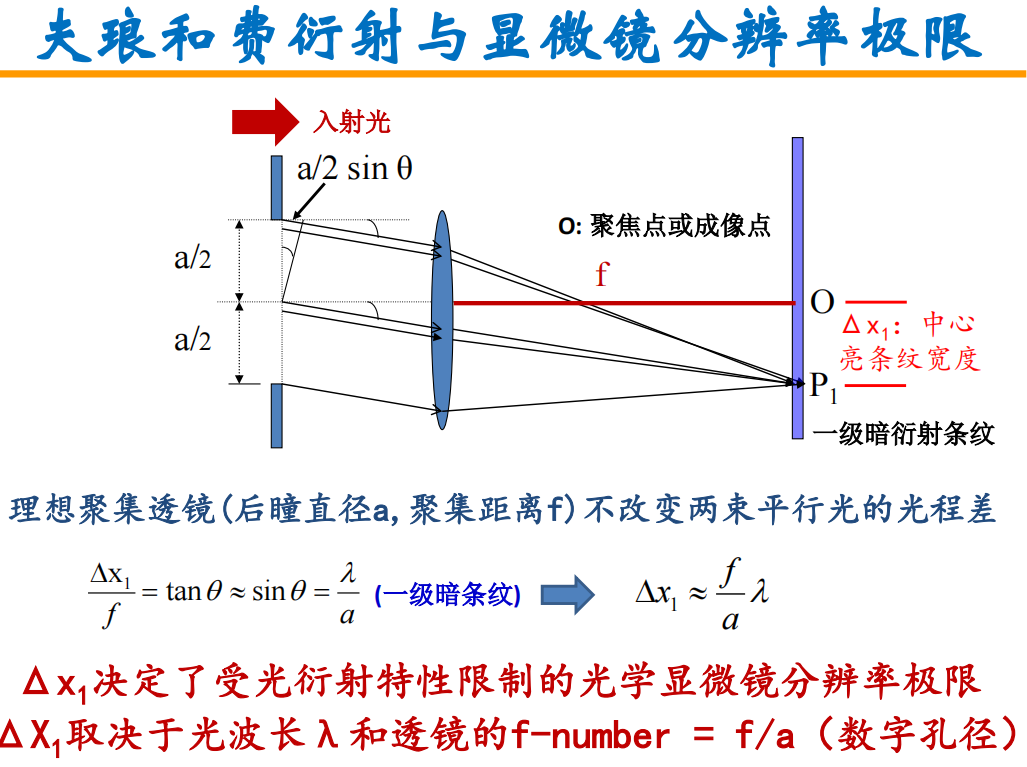   • 显微镜分辨率的基础：夫琅禾费衍射显微镜分辨率极限：数字孔径线分辨率与角分辨率：

艾里斑和显微镜分辨率

1. 艾里斑产生的原因以及光强分布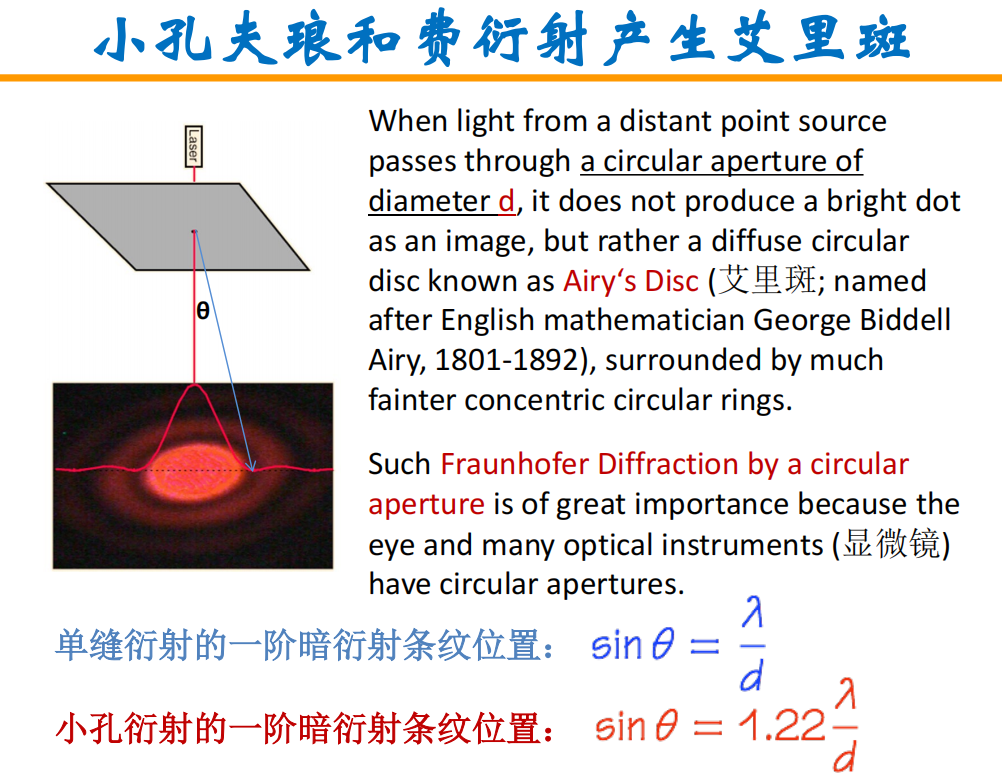：显微镜成像：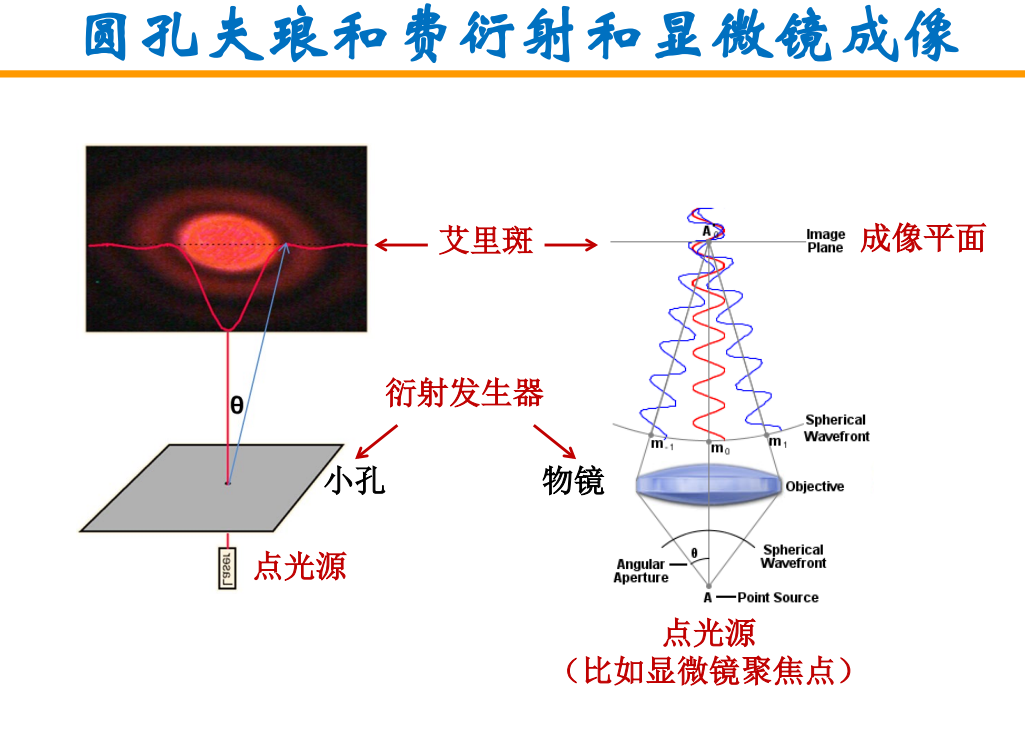
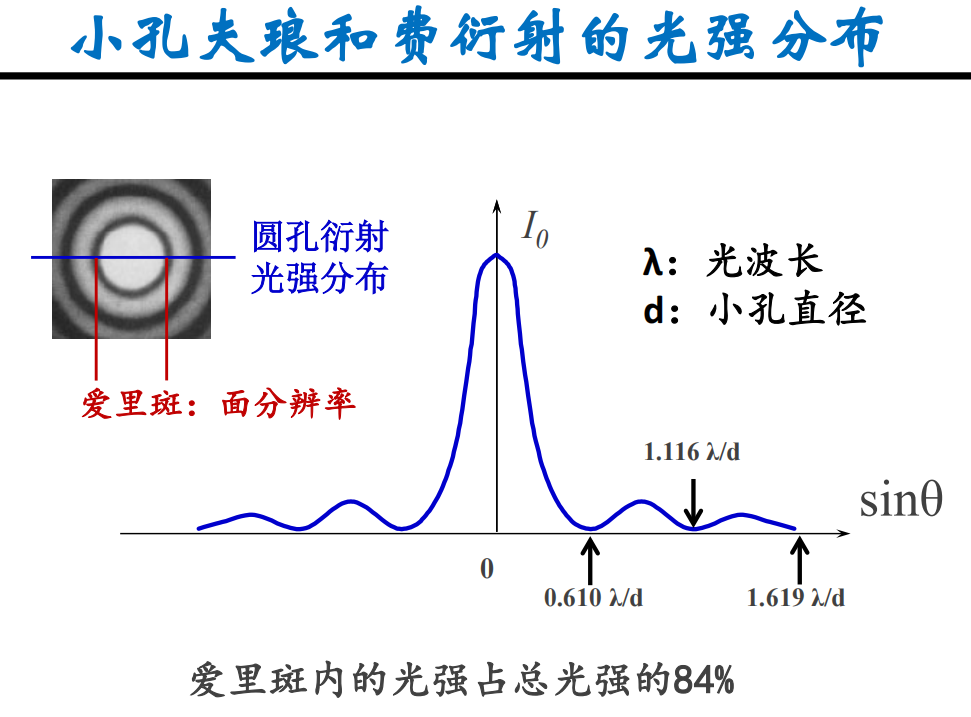
2. 显微镜的分辨率：
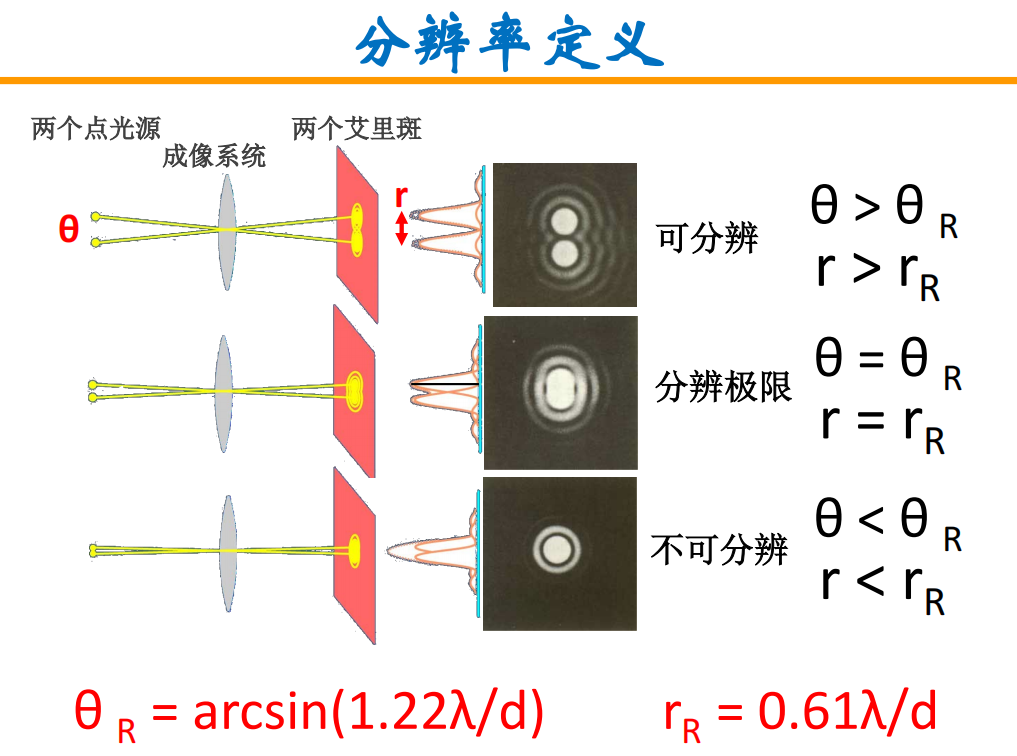
   1. 角分辨率：以最小的角度分离两个点光源
   2. 线分辨率(雷利规则)：相邻的两个艾里盘的最小距离是，一个衍射图案的中心最大值与另一个衍射图案的第一个最小值重合。
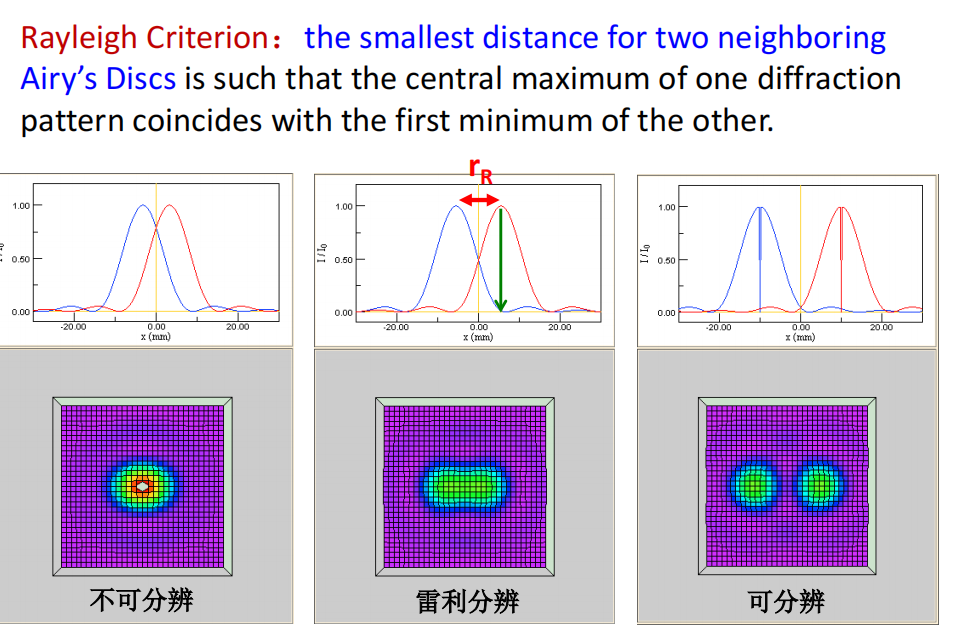
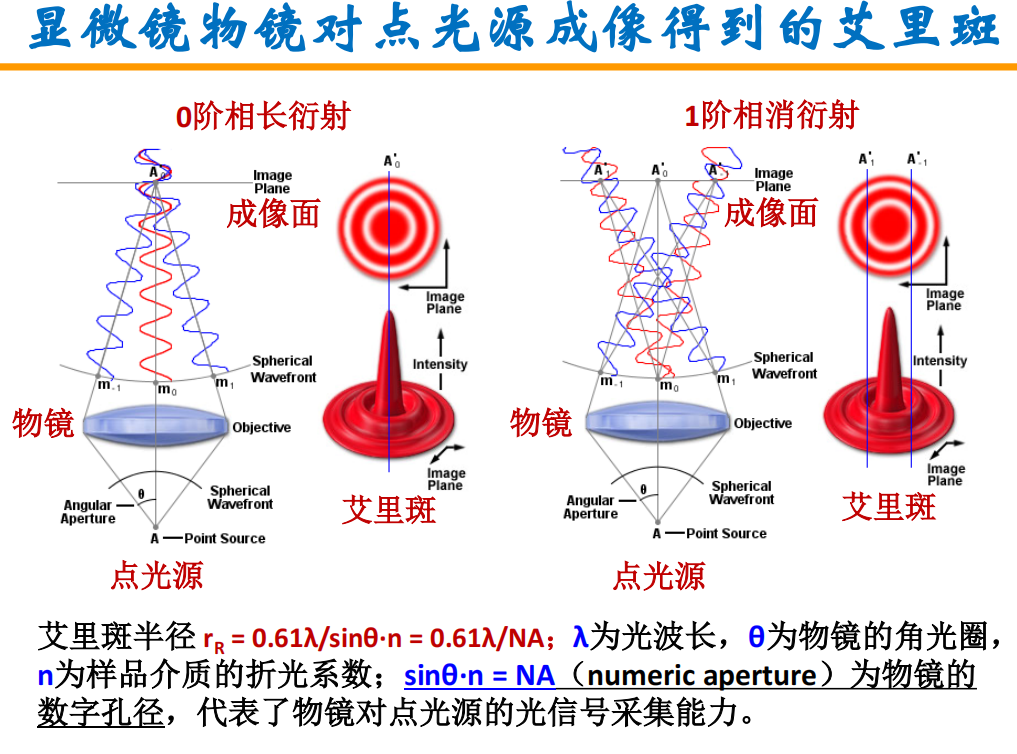   3. 光学显微镜的阿贝分辨率极限：注：NA与透镜数字孔径有关！分辨率与放大倍数的关系：
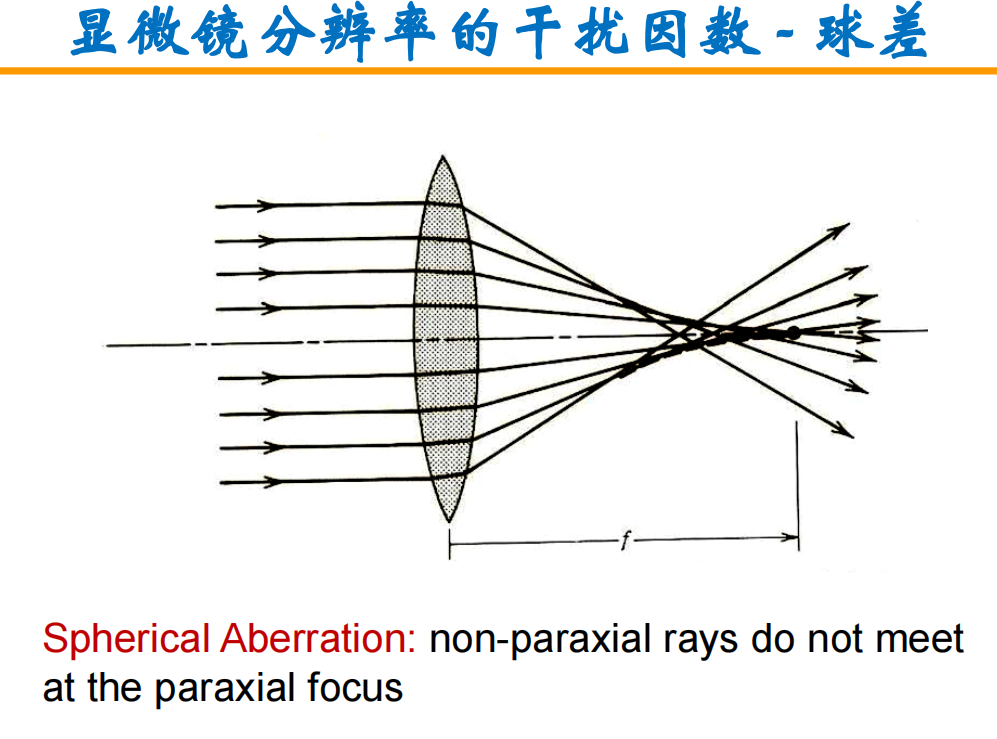
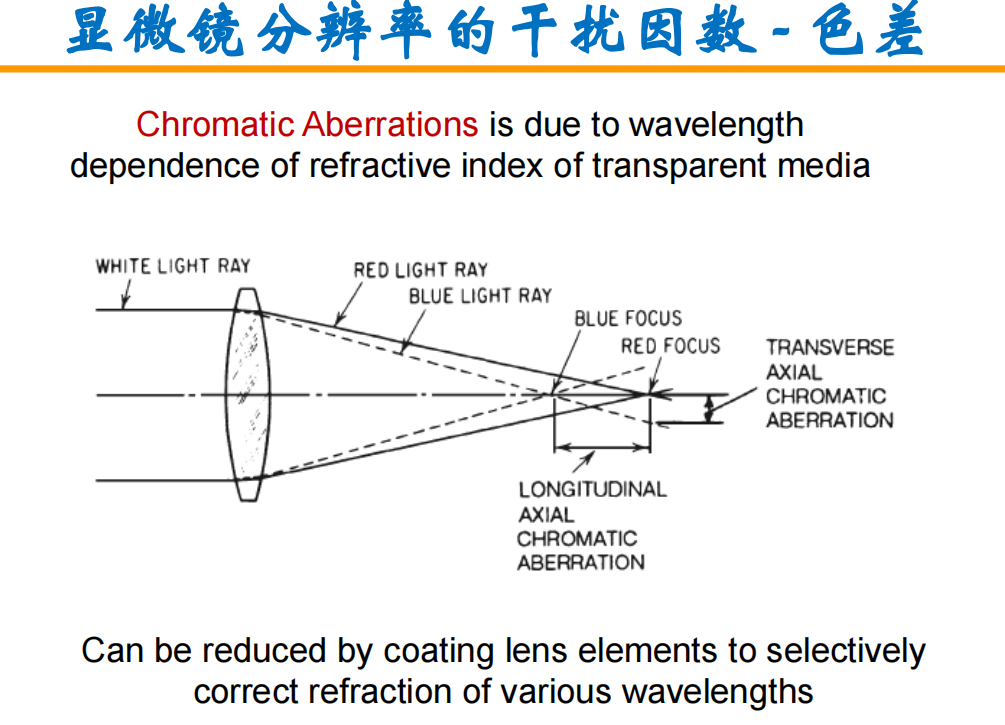
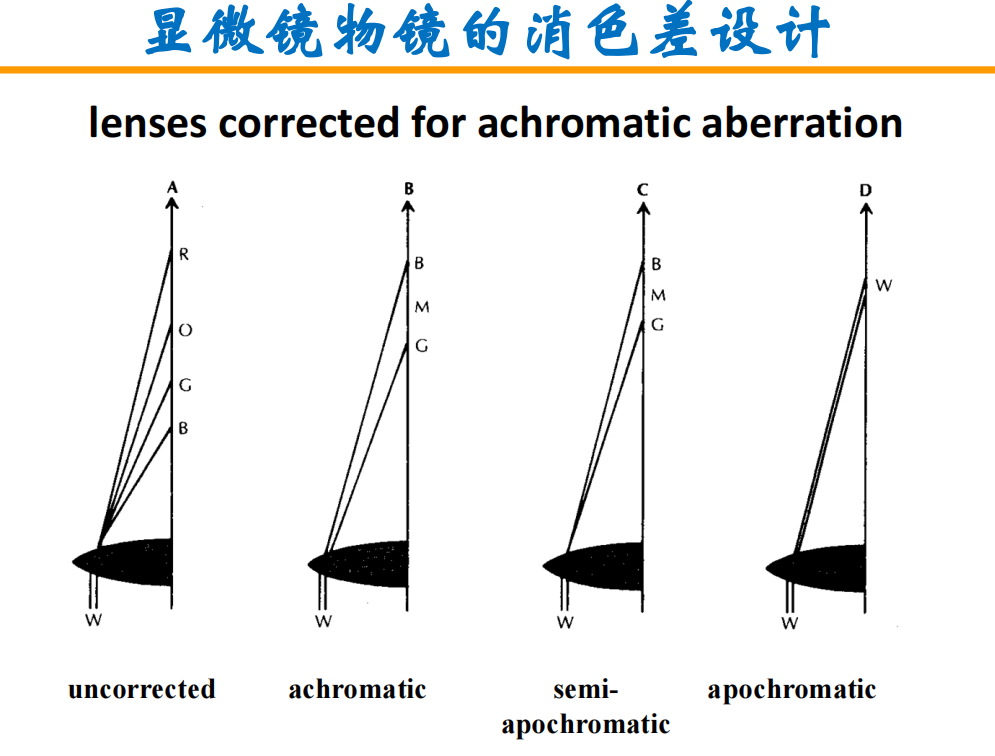
   4. 显微镜分辨率的干扰因数：完美的成像是无球差和无色差的！
      1. 球差：聚焦点不在一起
      2. 色差：不同波长光聚焦点不同
      3. 盖玻片厚度：注：由于油镜的折光系数n也为1.5，因此油镜通常不需要用盖玻片的调节环（通常可调节0.12mm-0.21mm的盖玻片）
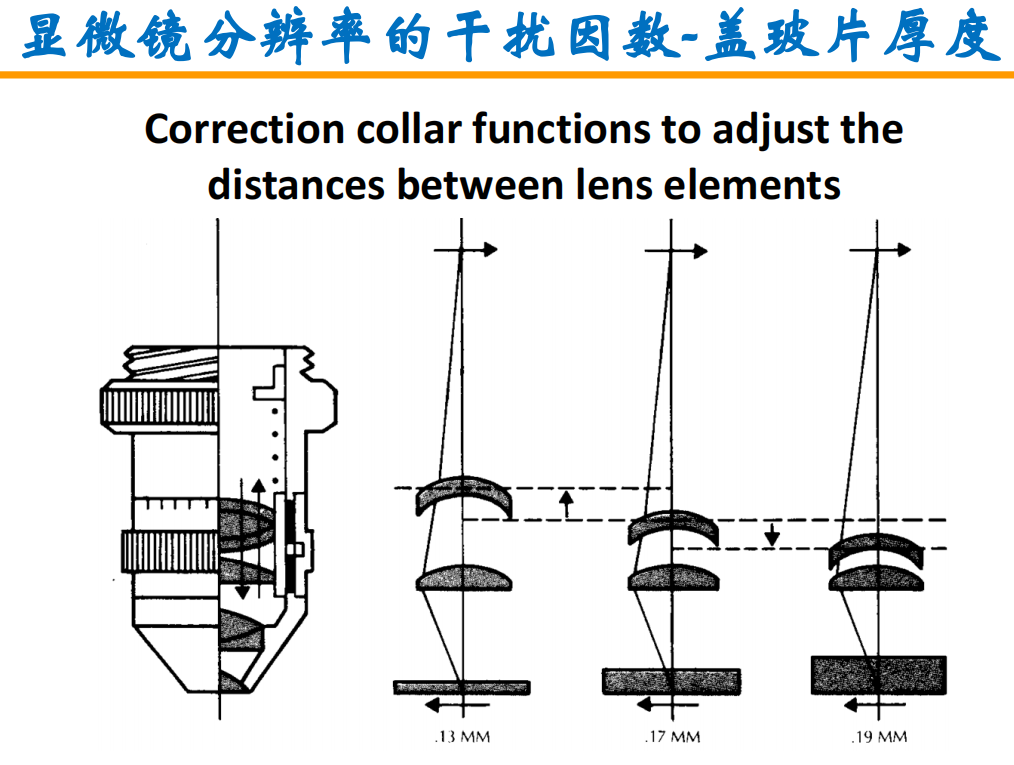
   5. 显微镜参数解读：注：∞的意思指的是光源经过物镜时为平行光；WD的意思是样品的厚度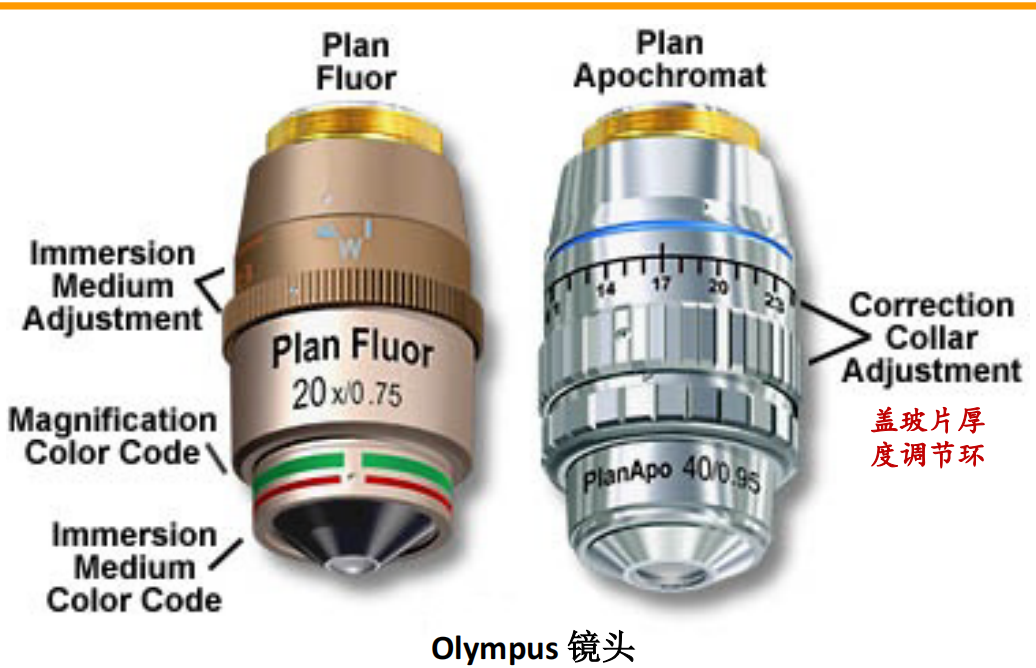注：Plan Fluor的作用是消色差！

点扩散函数和显微镜成像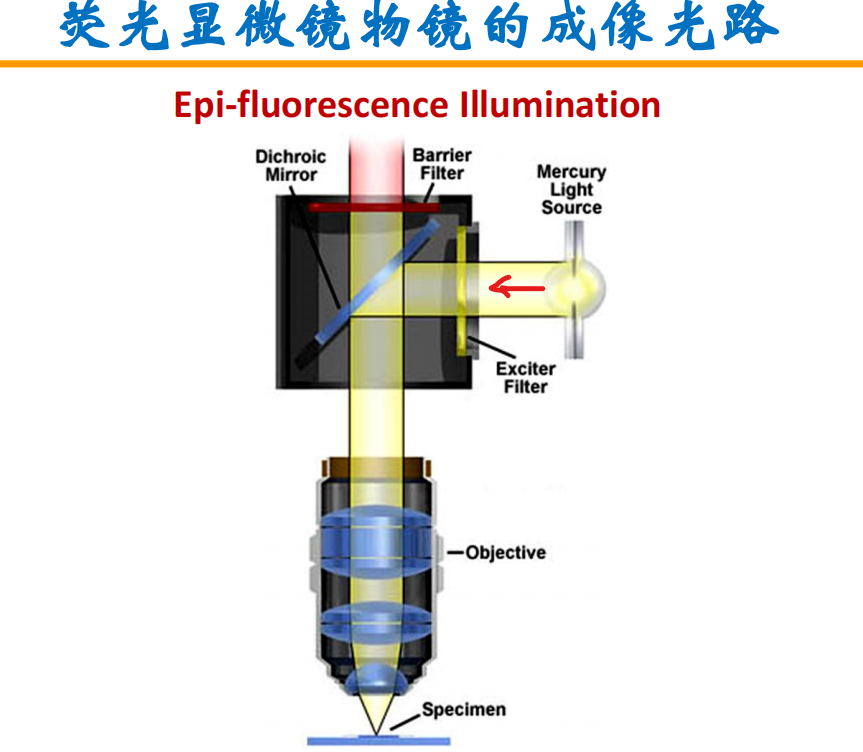

1. 点扩散函数(PSF)： ^fca9b3
   1. PSF与显微分辨率的关系:特定显微镜系统对一个点光源（比如远小于显微镜分辨率的单个荧光分子）三维成像得到的就是实验测得点扩散函数(下图所示)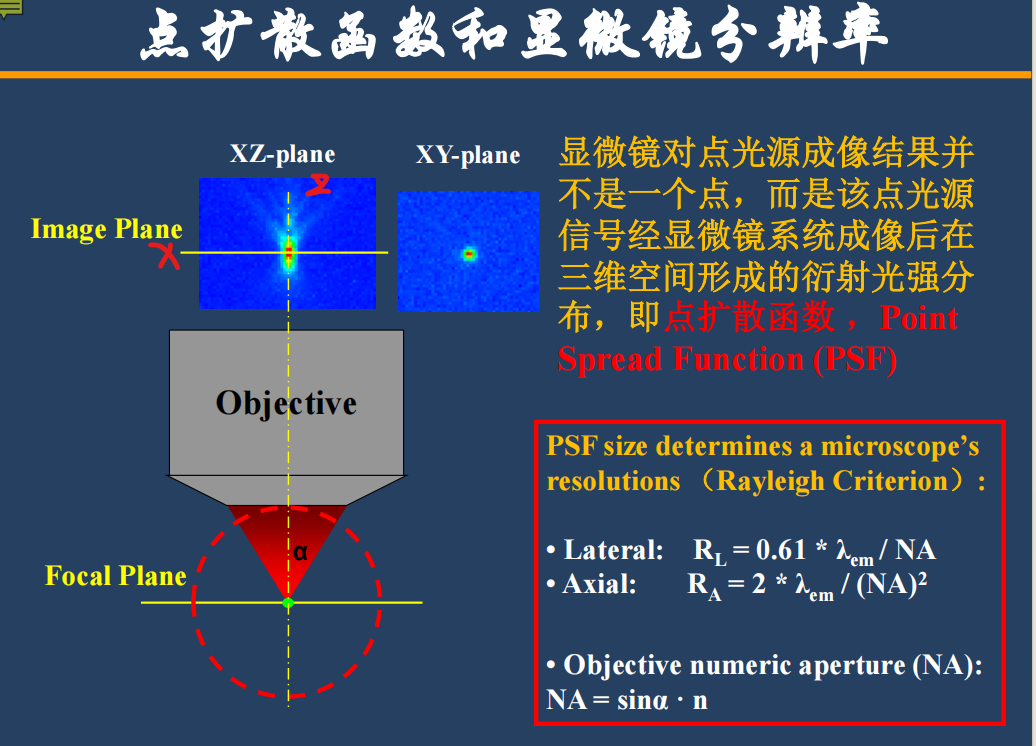注：XY平面的即是艾里斑，符合横向分辨率(Lateral)
      • 成像过程中的数学表达：无数点光源与其点扩散函数卷积的集合
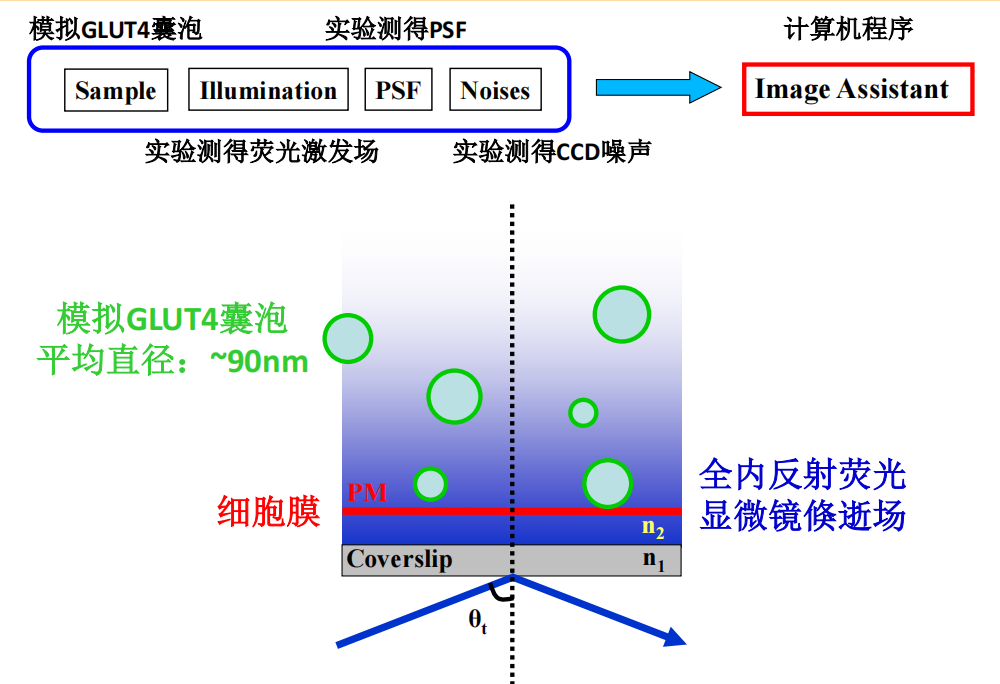
        • 例：囊泡注：通过测出的PSF、噪声以及像素，模拟出的囊泡与实际基本相似；此外通过反卷积，亦可把模糊的图像清晰化(提高分辨率的手段)！
   2. 显微技术发展探讨(超分辨技术的实现)：

傅里叶转换和光学传递函数

1. 傅里叶转换： ^77e568
   1. 频率：
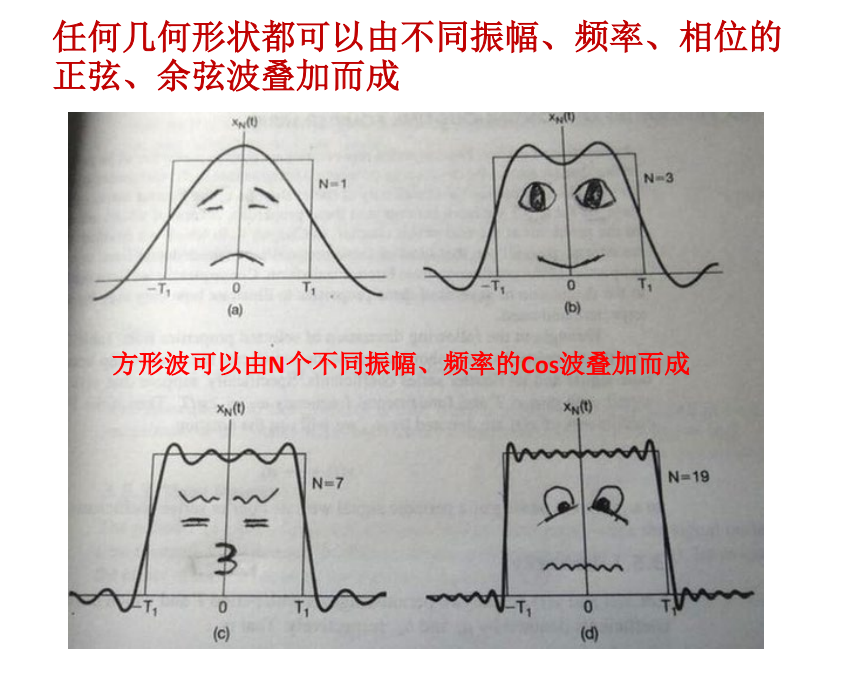
   2. 波的叠加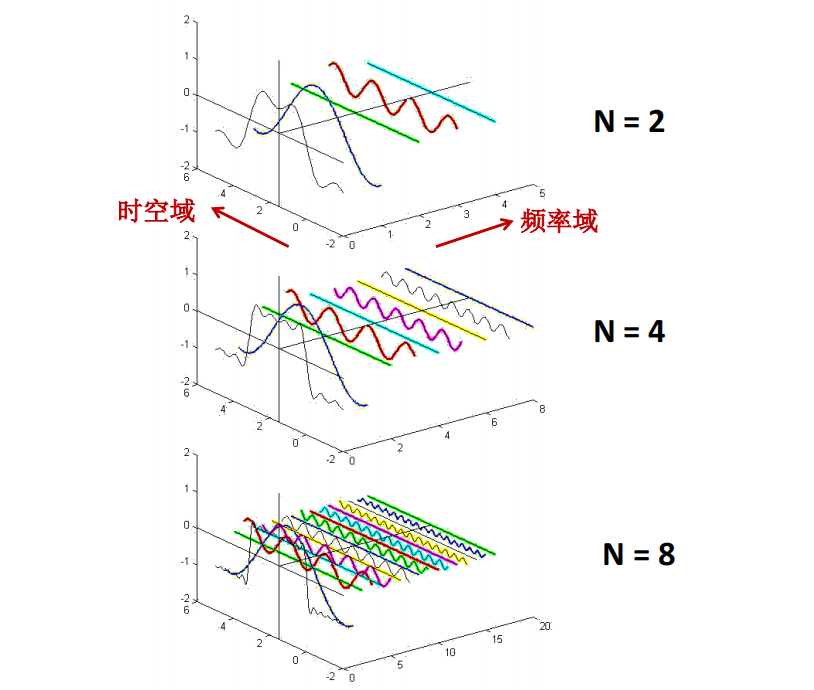：注：向量的圆周运动产生正弦/余弦波: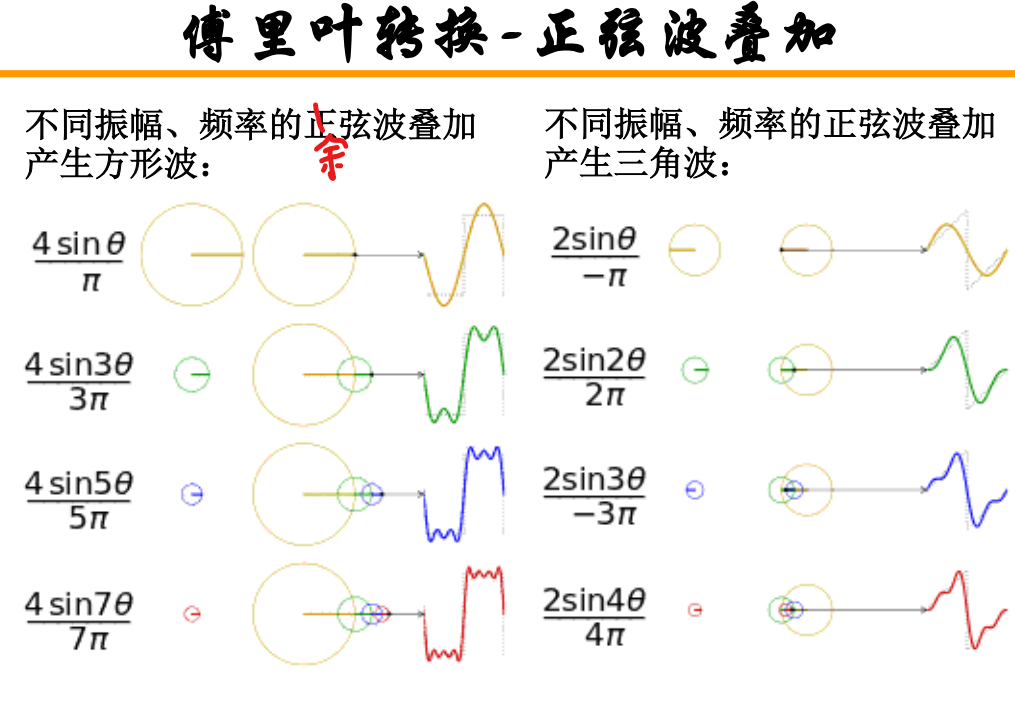
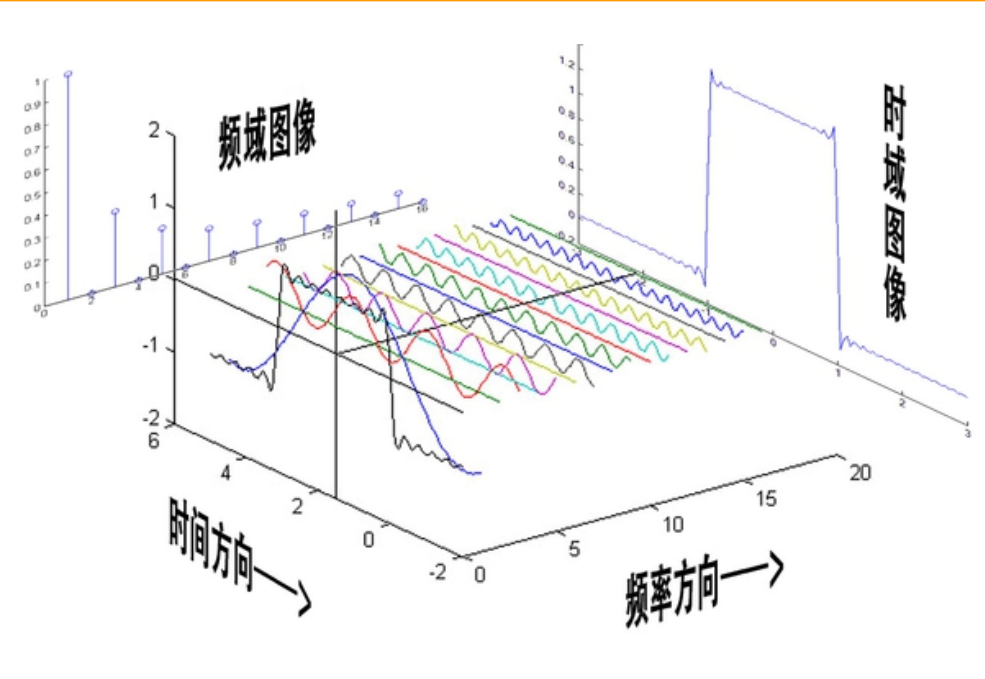
   3. 时空域(X轴)与频率域(Y轴)的转换:注：为何方形波边缘看着略高，是因为边缘处需要更高频的正弦/余弦波。
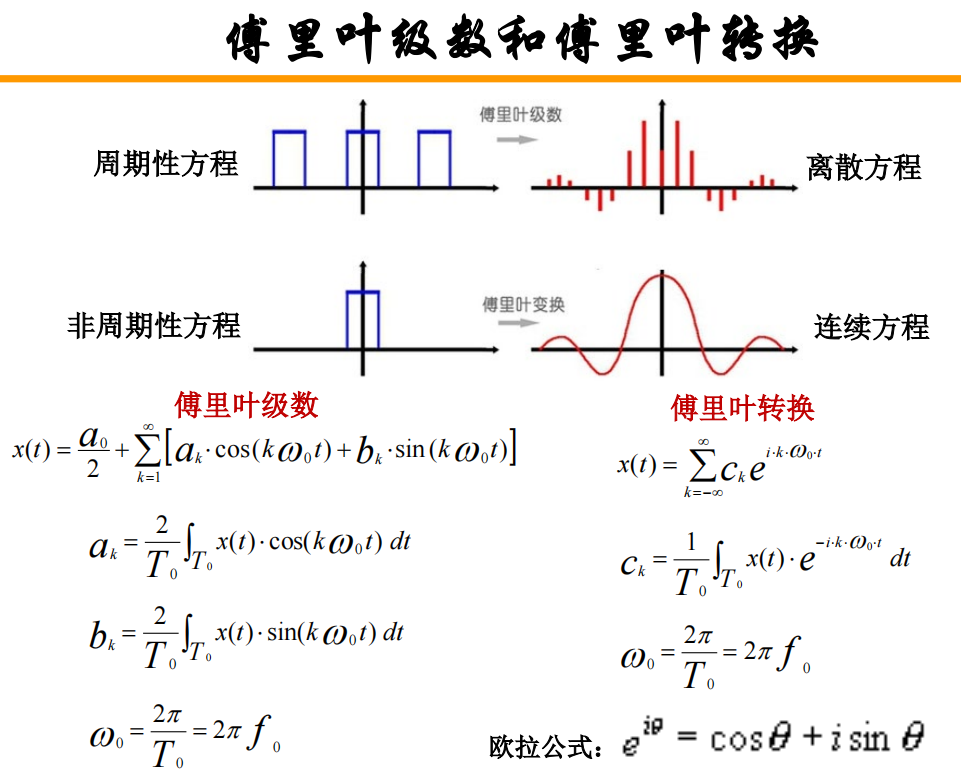
   4. 傅里叶级数与傅里叶转换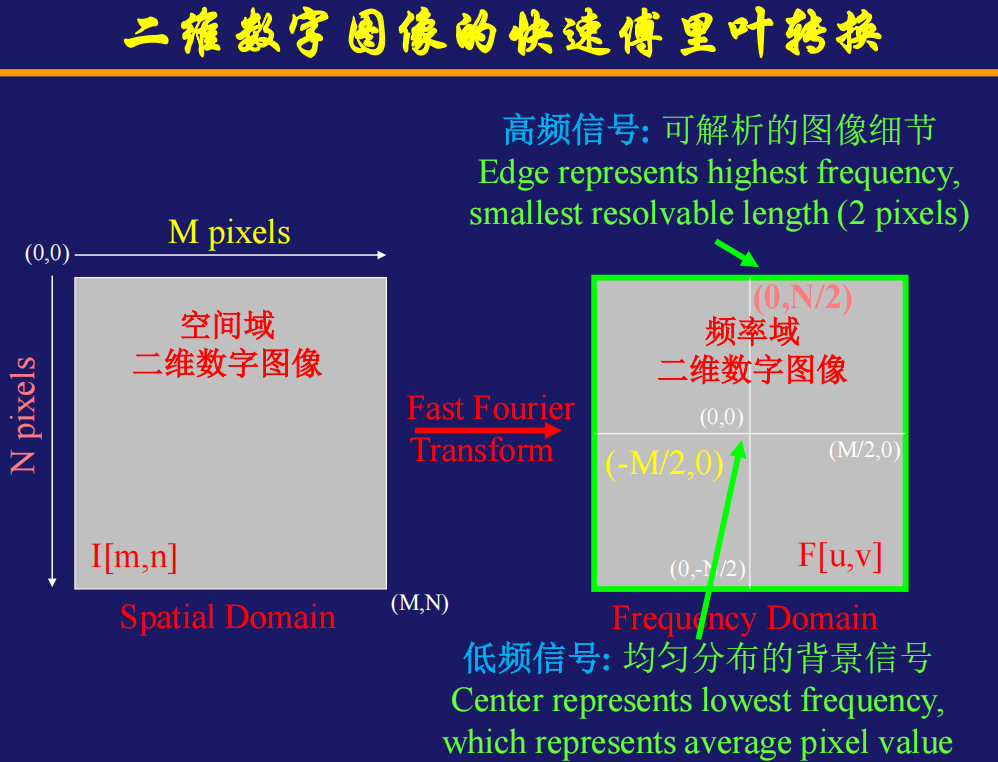：注：空间域的二维数字图像是离散的非周期性方程，转换后变成了连续方程，这样便于分析图像的特殊信号，即解析图像细节；例如：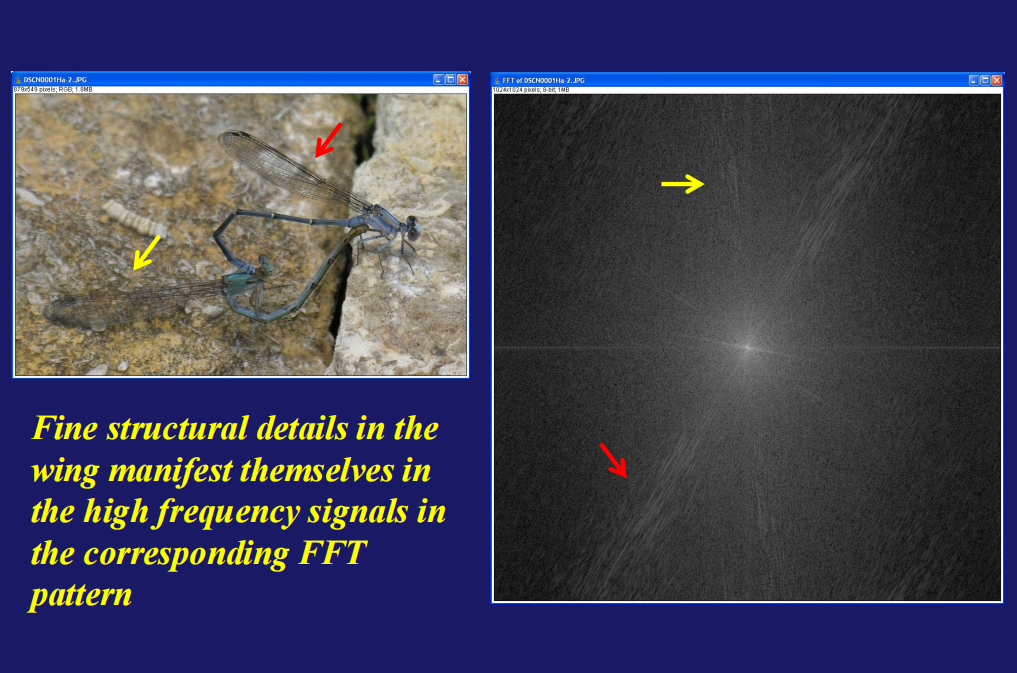
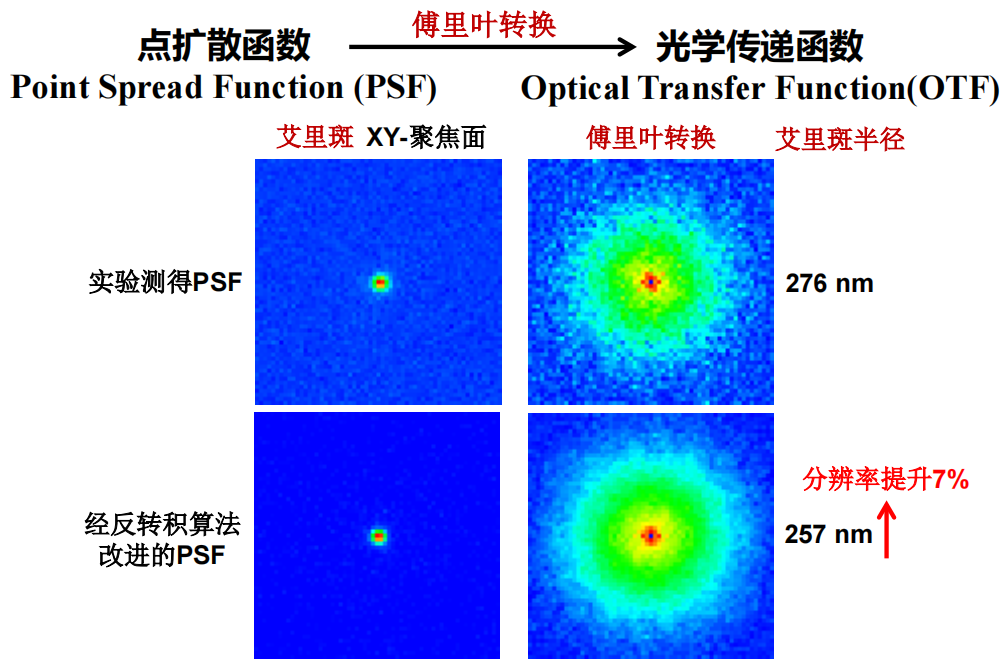
      • 点扩散函数和光学传递函数(OTF)：PSF经过傅里叶变换后使得艾里斑半径变大，里面的高频信号被放大，因此分辨率得到了提升。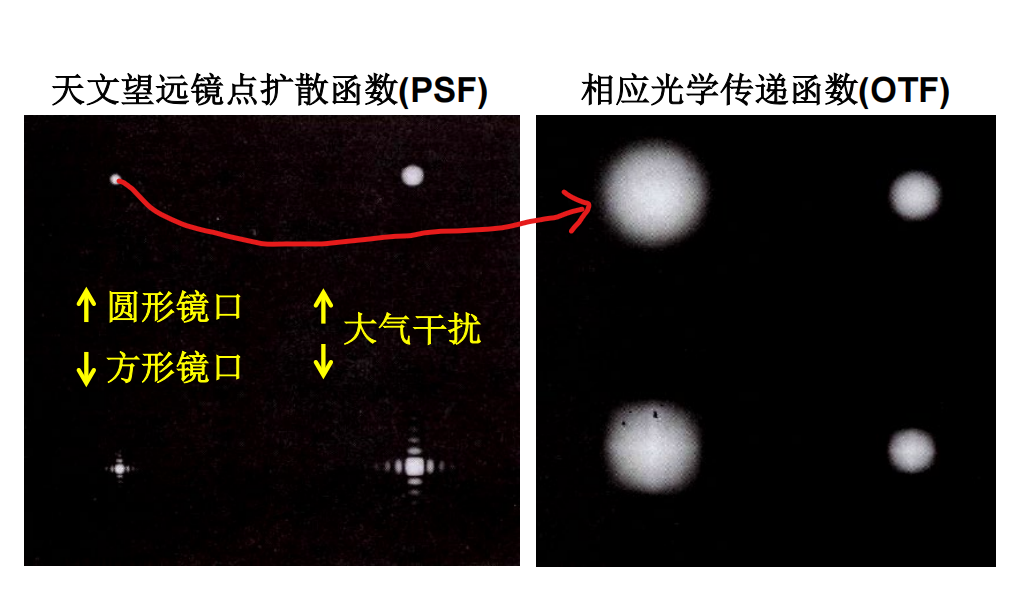注：左边的点分辨率更高，经过傅里叶转换分辨率提升的更多
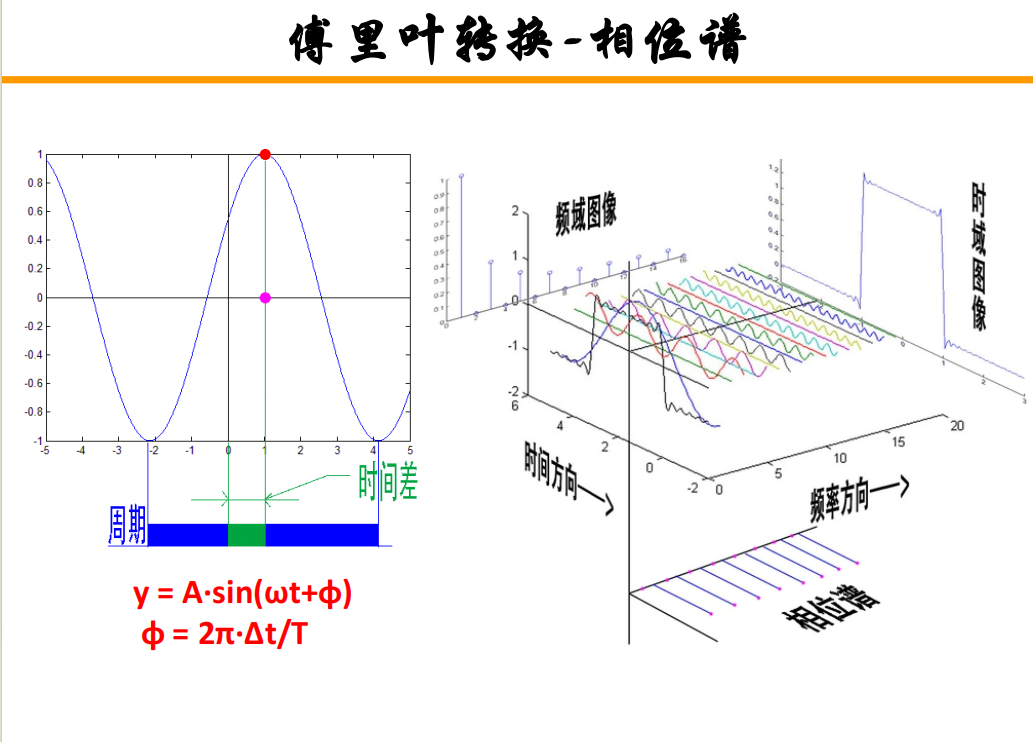
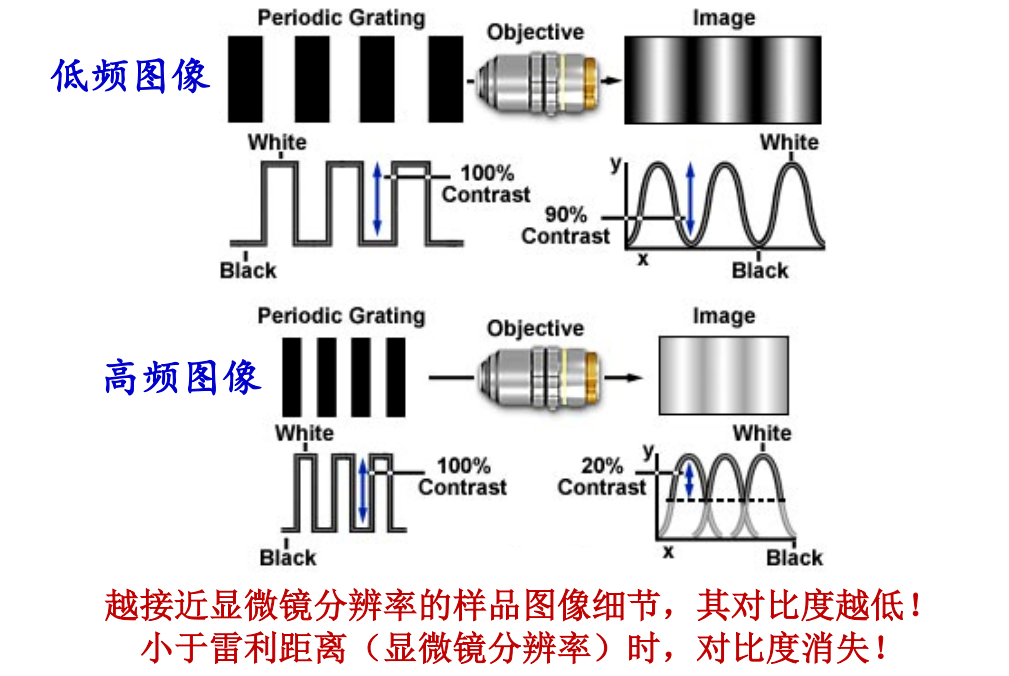      • 调制传递函数：注：截止频率越大，分辨率越高注：高频图像相较于低频图像的波长更短，这导致光源越接近；对比度消失时抵达截止频率，频率合计为0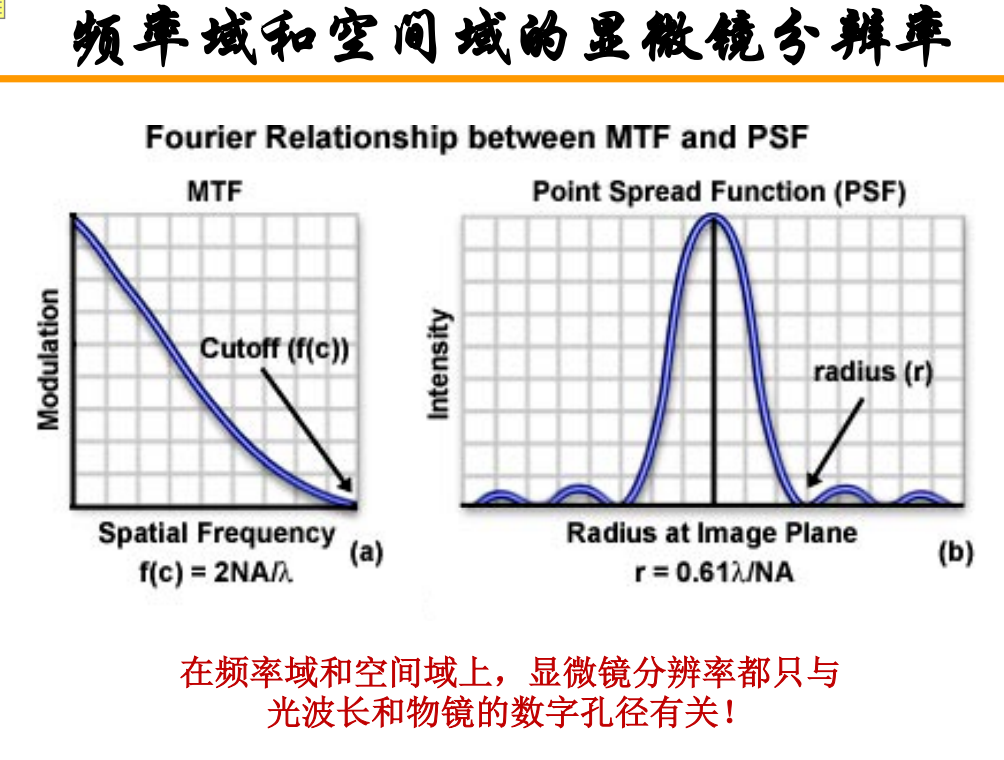注：频域率与分辨率的关系代表截止频率，与空间域的关系代表艾里斑。

总结