Motivating example
- 回顾：之前所有的state还有action是基于表格的形式——qπ(s,a)【编程的时候就把这些表格存储成向量矩阵或者是数组】
注：但表格不能处理较大且连续数量的state！【缺乏一定的泛化能力——很多值其实可以通过泛化来减少计算量——值函数近似】
- 值函数近似例子：利用一条直线来拟合很多点【这相当于通过一条直线来拟合大量数据】
注：优势在于不需要存储很多state value，只需要保存w两个参数；但近似不是特别精确
注：曲线拟合如下【更复杂的曲线需要存储更多的值：但拟合的精度更高】；v针对w任然是线性函数。
- 总结：用函数来拟合vπ(s)——减少存储、泛化能力【只访问一些状态，相邻的状态的值也可以比较准确的被估计出来】
估计状态价值的函数
- Objective function【目标函数】：找最优w使得估计的v接近真实的v【policy evaluation】
- 关于S的分布
- 均匀分布【实际很难均匀：比如希望给主要的状态更大的权重】：
- Stationary distribution【long-run后趋向于平稳】：dπ(s)【也代表agent平稳的时候，访问某一状态的概率，如果s被访问的概率大，d就大】代表权重，权重越大，希望它与实际的误差更小
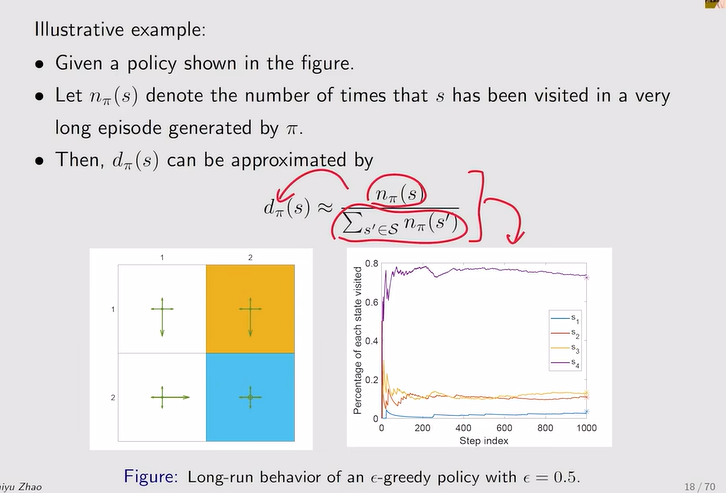
- 目标函数的优化：求梯度——随机梯度
注：vπ(St)未知——蒙特卡洛【当前状态得到的episode的一系列的reward——gt】/TD
- Function approximators【V估计的选择】：
- 线性：TD-linear【需要选取很好的特征向量Φ】
- 例：更多的参数得更好的拟合效果【但参数个数很多那和tabular也没区别，也是一样的复杂，并且增加参数也不可能使得误差为0】
注：我们此时需要用函数得到一个和基于模型用贝尔曼算出真实state value所得到的类似的曲面——越接近越好！
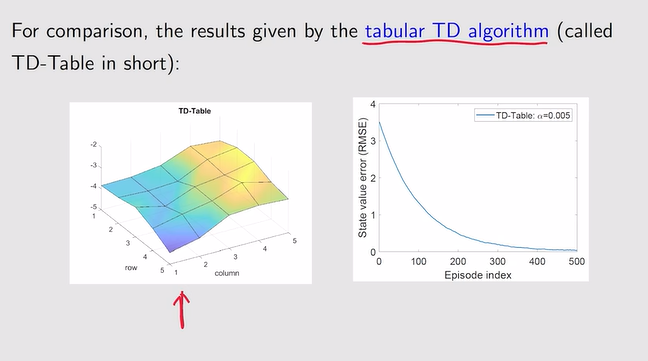
注：平面只能大致拟合一个趋势——因此需要用复杂的高阶曲面来拟合
- 总结：
Sarsa 和Q-learning
- Sarsa算法的结合：q替换了v
- 例：
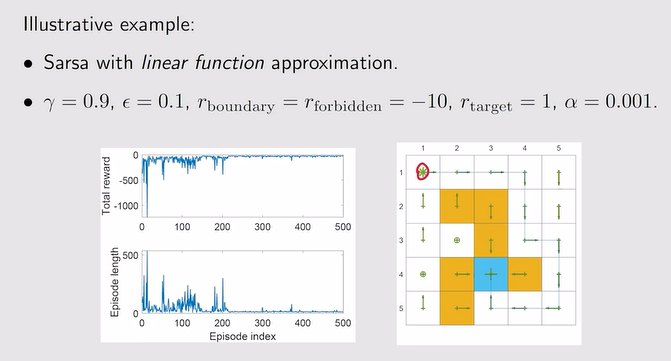
- Q-learning的结合：需要进行梯度计算
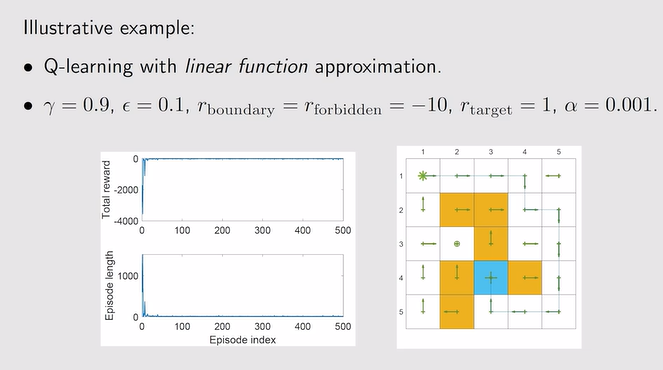
Deep Q-learning
- 定义：深度神经网络【非线性函数】结合强化学习的算法
- 优化：
注：使用上述两个网络的原因——先固定wT然后更新w，后面再把w【main】赋值给wT继续更新
- 经验回放：收集经验的时候有先后顺序，但使用的时候不一定需要按照先后顺序——从集合中随机取样(均匀分布：一个sample可以采样多次)来训练神经网络【经验回放】
注：这里解释为什么要用均匀分布【没有先验知识需要均匀分布】
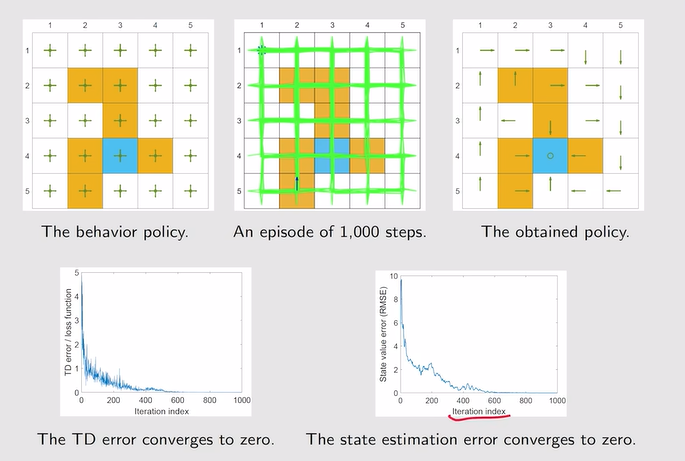
- 例：泛化能力+经验回放——有效减小了训练次数
注：这里的w是一个投影矩阵。