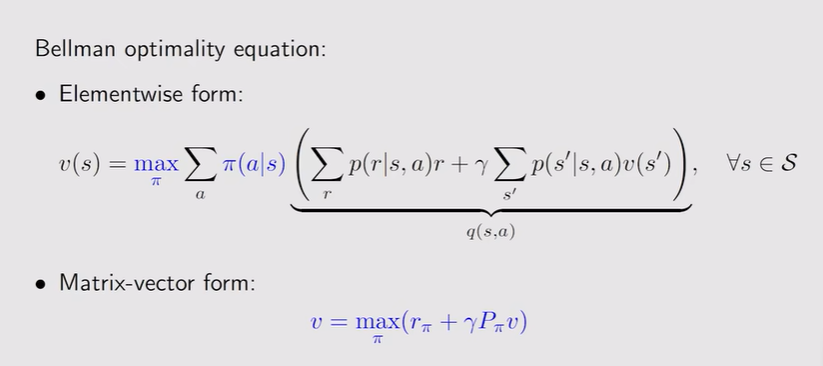Motivating examples
- State value+action value——线性方程组


- 当前策略不好时,如何提升?

 注:a* 代表action value最大的action!——不断迭代下去,即便一开始的策略很差,也会慢慢逼近最优策略
注:a* 代表action value最大的action!——不断迭代下去,即便一开始的策略很差,也会慢慢逼近最优策略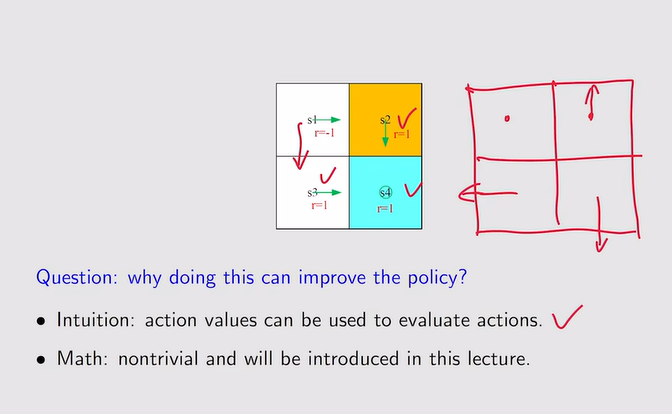 注:数学形式——贝尔曼最优公式
注:数学形式——贝尔曼最优公式
贝尔曼最优公式
-
最优策略:对于任意状态下采取的策略所产生的state value都要比其他的策略大,说明就是最优策略π*

-
贝尔曼最优公式:


-
表达式的分析思路:


 注:这相当于我给最大的那个action value赋予最大的权重,即为1
注:这相当于我给最大的那个action value赋予最大的权重,即为1 -
贝尔曼公式的重写:需要固定v才能求解一个maxπ,一次max是一个关于v的函数

-
Contraction mapping theorem:
- 不动点:f(x)是x的映射,若f(x)=x,代表我又映射到了我自己,这个点不再动,所以叫做不动点
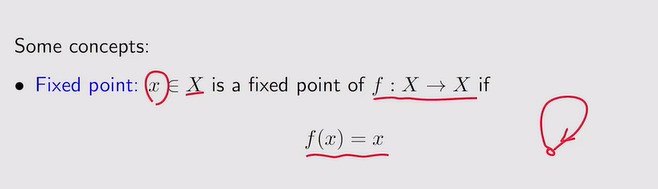
- Contraction mapping:


 注:通过迭代,Xk会趋向于不动点
注:通过迭代,Xk会趋向于不动点 - 例:
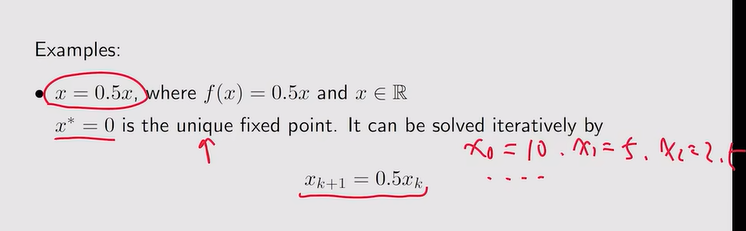
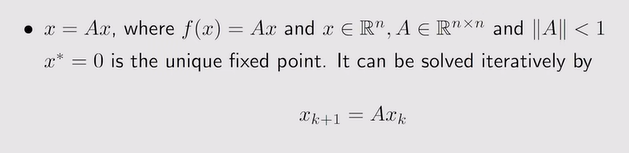 注:X是一个向量,A是一个矩阵
注:X是一个向量,A是一个矩阵
- 不动点:f(x)是x的映射,若f(x)=x,代表我又映射到了我自己,这个点不再动,所以叫做不动点
-
BOE的收缩性【收敛性】:



 注:value iteration algorithm【值迭代】
注:value iteration algorithm【值迭代】- 例:
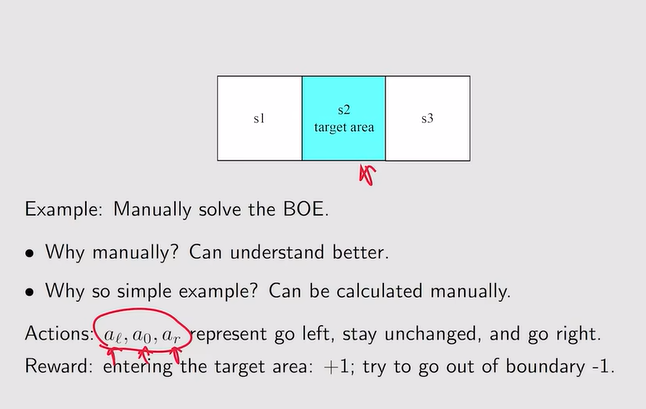
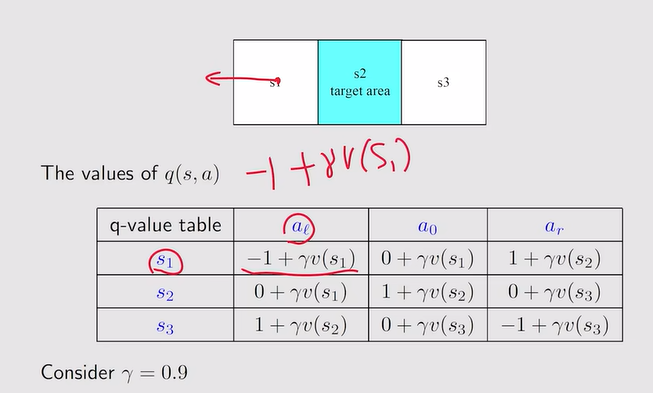
 注:贪婪策略选择最大的q-value
注:贪婪策略选择最大的q-value 注:ε为很小的数
注:ε为很小的数
- 例:
-
贝尔曼最优公式解的最优性:贝尔曼最优公式是贝尔曼公式的特殊,所对应的策略为π*【确定的但不唯一;state value是唯一的】


 注:π* 是确定的且贪婪的【选择p-value最大的】
注:π* 是确定的且贪婪的【选择p-value最大的】
最优策略的分析
- 什么样的因素决定了最优策略?【红色已知,求解黑色】——由模型+r+γ决定【往往调整r和γ,模型不好调整】

- γ的调整:
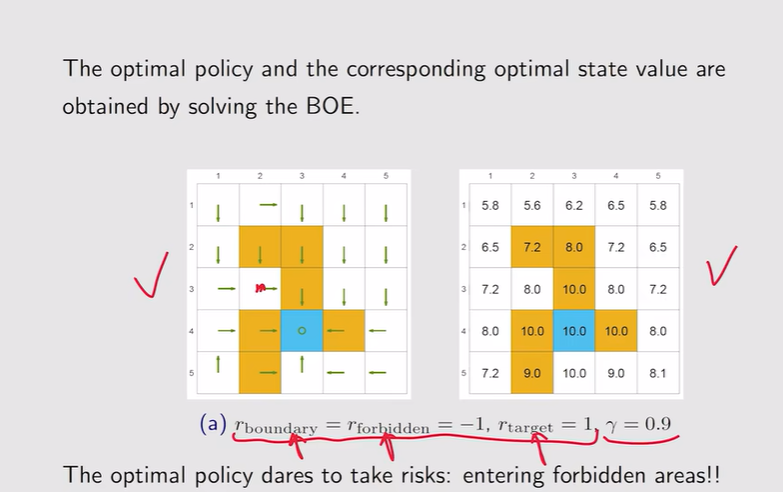 注:有时候最优策略不一定就完全绕开forbidden areas
注:有时候最优策略不一定就完全绕开forbidden areas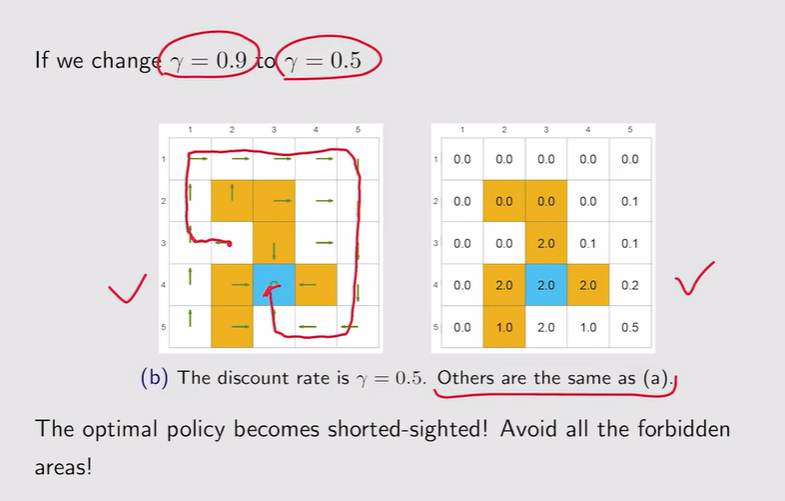 注:γ越大【远视】;γ较小【近视】
注:γ越大【远视】;γ较小【近视】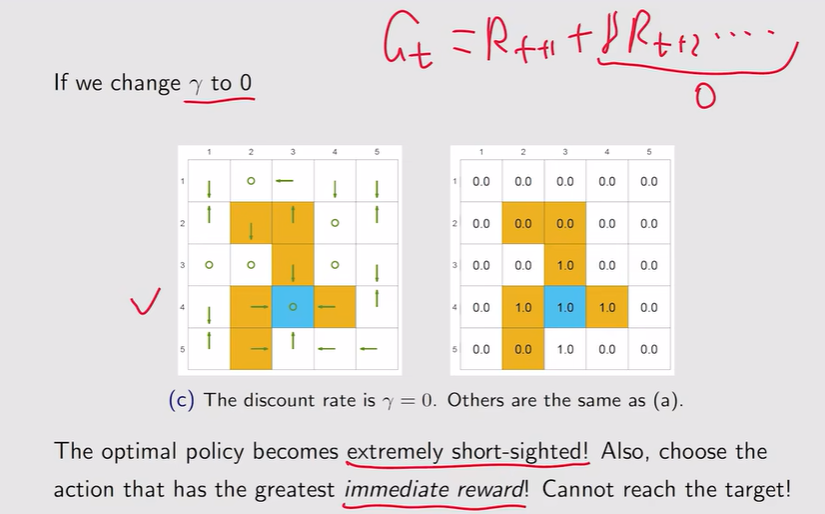 注:γ=0,整个策略变得非常短视
注:γ=0,整个策略变得非常短视 - r的调整:如果惩罚较大,他会直接绕开forbidden area

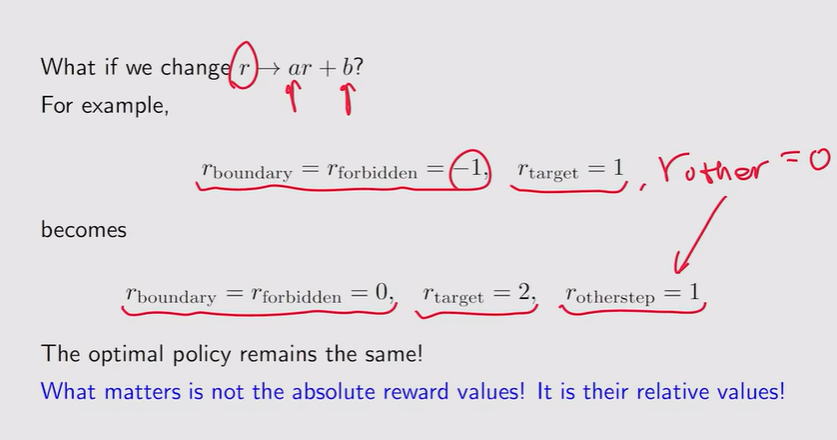 注:相对value不变就不会改变最终的最优策略【不看绝对值】
注:相对value不变就不会改变最终的最优策略【不看绝对值】
- 例:γ的约束可以避免绕路

- γ的调整: